Αρχιμήδεια ιδιότητα
| Το λήμμα δεν περιέχει πηγές ή αυτές που περιέχει δεν επαρκούν. |
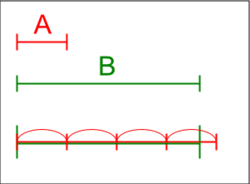
Η Αρχιμήδεια ιδιότητα στο σύνολο των πραγματικών αριθμών, δηλώνει ότι για όλους τους πραγματικούς αριθμούς x και y με x > 0, υπάρχει φυσικός αριθμός ν τέτοιος ώστε .
Η απόδειξη της ιδιότητας αυτής προκύπτει εύκολα από το γεγονός ότι το σύνολο N των φυσικών αριθμών δεν είναι άνω φραγμένο. Επειδή λοιπόν το N δεν είναι άνω φραγμένο ο πραγματικός αριθμός y/x δεν μπορεί να είναι άνω φράγμα του και επομένως υπάρχει τουλάχιστον ένας φυσικός αριθμός ν τέτοιος ώστε > y/x και ισοδύναμα .
Η γεωμετρική ερμηνεία της αρχιμήδειας ιδιότητας είναι η εξής: για οποιαδήποτε δύο ευθύγραμμα τμήματα, με ένα πεπερασμένο αριθμό ευθυγράμμων τμημάτων ίσων με το μικρότερο από τα δύο, τοποθετημένα το ένα δίπλα στο άλλο μπορούμε να σχηματίσουμε ευθύγραμμο τμήμα που να ξεπερνά το μεγαλύτερο από τα δύο σε μήκος.
Ιστορία και προέλευση του ονόματος της Αρχιμήδους ιδιότητας[Επεξεργασία | επεξεργασία κώδικα]
Η συγκεκριμένη έννοια έλαβε το όνομά της από τον Ότο Στολτς (στη δεκαετία του 1880) από τον αρχαίο Έλληνα γεωμέτρη και φυσικό Αρχιμήδη από τις Συρακούσες.
Η Αρχιμήδεια ιδιότητα εμφανίζεται στο βιβλίο V των Στοιχείων του Ευκλείδη ως Ορισμός 4:
Λέγεται ότι τα μεγέθη έχουν λόγο μεταξύ τους που μπορούν, όταν πολλαπλασιάζονται, να υπερβαίνουν το ένα το άλλο.
Επειδή ο Αρχιμήδης το απέδωσε στον Εύδοξο της Κνίδου, είναι επίσης γνωστό ως "Θεώρημα του Εύδοξου" ή αξίωμα του Εύδοξου[1].
Ο Αρχιμήδης χρησιμοποίησε τα απειροστά σε ευρετικά επιχειρήματα, αν και αρνήθηκε ότι αυτά ήταν τελειωμένες μαθηματικές αποδείξεις.
Ορισμός για γραμμικά διατεταγμένες ομάδες[Επεξεργασία | επεξεργασία κώδικα]
Έστω x και y θετικά στοιχεία μιας γραμμικά διατεταγμένης ομάδας G. Τότε το είναι απειροελάχιστο σε σχέση με το (ή ισοδύναμα, το είναι άπειρο σε σχέση με το ) αν, για κάθε φυσικό αριθμό , το πολλαπλάσιο είναι μικρότερο από το y, δηλαδή ισχύει η ακόλουθη ανισότητα:
Ο ορισμός αυτός μπορεί να επεκταθεί σε ολόκληρη την ομάδα με τη λήψη απόλυτων τιμών.
Η ομάδα είναι Αρχιμήδειος αν δεν υπάρχει ζεύγος τέτοιο ώστε το να είναι απειροελάχιστο ως προς το .
Επιπλέον, εάν το είναι μια αλγεβρική δομή με μονάδα (1) - παραδείγματος χάριν, ένας δακτύλιος - ένας παρόμοιος ορισμός ισχύει για το . Αν το είναι απειροελάχιστο ως προς το , τότε το είναι ένα απειροελάχιστο στοιχείο. Ομοίως, αν το είναι άπειρο ως προς το , τότε το είναι ένα άπειρο στοιχείο. Η αλγεβρική δομή είναι Αρχιμήδειος αν δεν έχει άπειρα στοιχεία και δεν έχει απειροελάχιστα στοιχεία.
Παραπομπές[Επεξεργασία | επεξεργασία κώδικα]
- ↑ Knopp, Konrad (1951). Theory and Application of Infinite Series
 (English 2nd έκδοση). London and Glasgow: Blackie & Son, Ltd. σελ. 7. ISBN 0-486-66165-2.
(English 2nd έκδοση). London and Glasgow: Blackie & Son, Ltd. σελ. 7. ISBN 0-486-66165-2.
| Αυτό το μαθηματικό λήμμα χρειάζεται επέκταση. Μπορείτε να βοηθήσετε την Βικιπαίδεια επεκτείνοντάς το. |










