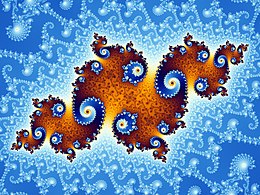
Σύνολο Μάντελμπροτ

Το σύνολο Μάντελμπροτ είναι ένα μαθηματικό φράκταλ που ορίζεται από τον αναδρομικό τύπο z = z^2 + c, όπου z και c είναι μιγαδικοί αριθμοί. Αυτή η εικόνα υπολογίστηκε για 100.000 επαναλήψεις χρησιμοποιώντας το δωρεάν πρόγραμμα Fractal Explorer 2.02. Όρια παραθύρου: -2<Re(c)<0,5 και -0,9375<Im(c)<0,9375

Μεγέθυνση

Το Σύνολο Μάντελμπροτ είναι ένα δισδιάστατο σύνολο με έναν σχετικά απλό ορισμό που παρουσιάζει μεγάλη πολυπλοκότητα, ειδικά καθώς μεγεθύνεται. Είναι δημοφιλές για την αισθητική του και τις µορφοκλασµατικές δοµές του. Το σύνολο ορίζεται στο μιγαδικό επίπεδο ως οι μιγαδικοί αριθμοί $c$ για τους οποίους η συνάρτηση $f_{c}(z)=z^{2}+c$ δεν αποκλίνει στο άπειρο όταν η επανάληψη ξεκινά από το $z=0$, δηλ, για την οποία η ακολουθία $f_{c}(0)$, $f_{c}(f_{c}(0))$, κ.λπ. παραμένει περιορισμένη στην απόλυτη τιμή.

Το σύνολο αυτό ορίστηκε και σχεδιάστηκε για πρώτη φορά από τους Ρόμπερτ Γ. Μπρουκς και Πίτερ Ματέλσκι το 1978, στο πλαίσιο μιας μελέτης των ομάδων Κλάιν. Στη συνέχεια, το 1980, ο Μπενουά Μάντελμπροτ απέκτησε υψηλής ποιότητας απεικονίσεις του συνόλου, ενώ εργαζόταν στο ερευνητικό κέντρο Τόμας Τζ. Γουάτσον στο Γιόρκταουν Χάιτς της Νέας Υόρκης.

Οι εικόνες του συνόλου Μάντελμπροτ παρουσιάζουν ένα απείρως περίπλοκο όριο που αποκαλύπτει προοδευτικά όλο και πιο λεπτομερείς αναδρομικές λεπτομέρειες σε αυξανόμενες μεγεθύνσεις. Μαθηματικά, το όριο του συνόλου Μάντελμπροτ είναι μια καμπύλη φράκταλ. Το "στυλ" αυτής της αναδρομικής λεπτομέρειας εξαρτάται από την περιοχή του ορίου του συνόλου που εξετάζεται. Οι εικόνες του συνόλου Μάντελμπροτ μπορούν να δημιουργηθούν με τη δειγματοληψία των μιγαδικών αριθμών και τον έλεγχο, για κάθε σημείο του δείγματος $c$, εάν η ακολουθία $f_{c}(0),f_{c}(f_{c}(0)),\dotsc$ πηγαίνει προς το άπειρο. Αντιμετωπίζοντας το πραγματικό και το φανταστικό μέρος του $c$ ως συντεταγμένες εικόνας στο μιγαδικό επίπεδο, τα εικονοστοιχεία μπορούν στη συνέχεια να χρωματιστούν ανάλογα με το πόσο σύντομα η ακολουθία $|f_{c}(0)|,|f_{c}(f_{c}(0))|,\dotsc$ διασχίζει ένα αυθαίρετα επιλεγμένο κατώφλι (το κατώφλι πρέπει να είναι τουλάχιστον 2, επειδή το -2 είναι ο μιγαδικός αριθμός με το μεγαλύτερο μέγεθος στο σύνολο, αλλά διαφορετικά το κατώφλι είναι αυθαίρετο). Αν το $c$ διατηρηθεί σταθερό και μεταβληθεί η αρχική τιμή του $z$, λαμβάνουμε το σύνολο Julia που αντιστοιχεί στο σημείο $c$.

Το σύνολο Μάντελμπροτ έχει γίνει δημοφιλές και εκτός των μαθηματικών, τόσο για την αισθητική του όσο και ως παράδειγμα σύνθετης δομής που προκύπτει από την εφαρμογή απλών κανόνων. Είναι ένα από τα πιο γνωστά παραδείγματα μαθηματικής οπτικοποίησης, μαθηματικού κάλλους και μοτίβου.

Ιστορία

Το σύνολο Μάντελμπροτ έχει τις ρίζες του στη σύνθετη δυναμική, ένα πεδίο που διερευνήθηκε για πρώτη φορά από τους Γάλλους μαθηματικούς Πιερ Φατού και Γκαστόν Τζούλια στις αρχές του 20ού αιώνα. Το φράκταλ ορίστηκε και σχεδιάστηκε για πρώτη φορά το 1978 από τους Ρόμπερτ Γ. Μπρουκς και Πίτερ Ματέλσκι στο πλαίσιο μιας μελέτης των ομάδων Κλάιν. Την 1η Μαρτίου 1980, στο ερευνητικό κέντρο Τόμας Τζ. Γουάτσον της IBM στο Γιόρκταουν Χάιτς της Νέας Υόρκης, ο Μπενουά Μαντελμπρότ οπτικοποίησε για πρώτη φορά το σύνολο.

Η πρώτη δημοσιευμένη εικόνα του συνόλου Μάντελμπροτ, από τους Ρόμπερτ Γ. Μπρουκς και Πίτερ Ματέλσκι το 1978.

Ο Μάντελμπροτ μελέτησε το χώρο παραμέτρων των τετραγωνικών πολυωνύμων σε ένα άρθρο που δημοσιεύτηκε το 1980. Η μαθηματική μελέτη του συνόλου Μάντελμπροτ ξεκίνησε πραγματικά με την εργασία των μαθηματικών Αντριέν Ντουαντί και Τζον Χ. Χάμπαρντ (1985) , οι οποίοι καθόρισαν πολλές από τις θεμελιώδεις ιδιότητές του και ονόμασαν το σύνολο προς τιμήν του Μάντελμπροτ για το επιδραστικό έργο του στη μορφοκλασματική γεωμετρία.

Οι μαθηματικοί Χάιντς-Όττο Πέιτγκεν και Πέτερ Ρίχτερ έγιναν γνωστοί για την προώθηση του συνόλου με φωτογραφίες, βιβλία (1986) και μια διεθνή περιοδεύουσα έκθεση του γερμανικού Ινστιτούτου Γκαίτε (1985).

Στο εξώφυλλο του περιοδικού Scientific American τον Αύγουστο του 1985 παρουσιάστηκε ο αλγόριθμος για τον υπολογισμό του συνόλου Μάντελμπροτ. Το εξώφυλλο δημιουργήθηκε από τους Πάιτγκεν, Ρίχτερ και Σάουπε στο Πανεπιστήμιο της Βρέμης. Το σύνολο Μάντελμπροτ έγινε γνωστό στα μέσα της δεκαετίας του 1980 ως επίδειξη γραφικών υπολογιστών, όταν οι προσωπικοί υπολογιστές έγιναν αρκετά ισχυροί για να σχεδιάσουν και να απεικονίσουν το σύνολο σε υψηλή ανάλυση.

Το έργο των Ντουάντι και Χάμπαρντ έλαβε χώρα σε μια εποχή που το ενδιαφέρον για τη σύνθετη δυναμική και τα αφηρημένα μαθηματικά αυξανόταν και η μελέτη του συνόλου Μάντελμπροτ αποτελεί έκτοτε ένα από τα κεντρικά σημεία αυτού του πεδίου.

Επίσημος ορισμός

Το σύνολο Μάντελμπροτ είναι το σύνολο των τιμών του c στο μιγαδικό επίπεδο για τις οποίες η τροχιά του κρίσιμου σημείου ${\textstyle z=0}$ υπό την επανάληψη του τετραγωνικού χάρτη

$z_{n+1}=z_{n}^{2}+c$

Έτσι, ένας μιγαδικός αριθμός c είναι μέλος του συνόλου Μάντελμπροτ αν, ξεκινώντας από $z_{0}=0$ και εφαρμόζοντας επανειλημμένα την επανάληψη, η απόλυτη τιμή του $z_{n}$ παραμένει περιορισμένη για όλα τα $n>0$

Παραδείγματος χάριν, για c = 1, η ακολουθία είναι 0, 1, 2, 5, 26, ..., η οποία τείνει στο άπειρο, οπότε το 1 δεν είναι στοιχείο του συνόλου Μάντελμπροτ. Από την άλλη πλευρά, για c = - 1 c=-1, η ακολουθία είναι 0, -1, 0, 0, -1, 0, ..., η οποία είναι περιορισμένη, οπότε το -1 ανήκει στο σύνολο.

Το σύνολο Μάντελμπροτ μπορεί επίσης να οριστεί ως ο τόπος συνδεσιμότητας της οικογένειας των τετραγωνικών πολυωνύμων $f(z)=z^{2}+c$, το υποσύνολο του χώρου των παραμέτρων $c$ για το οποίο το σύνολο Julia του αντίστοιχου πολυωνύμου σχηματίζει ένα συνδεδεμένο σύνολο. Κατά τον ίδιο τρόπο, το όριο του συνόλου Μάντελμπροτ μπορεί να οριστεί ως ο τόπος διακλάδωσης αυτής της τετραγωνικής οικογένειας, το υποσύνολο των παραμέτρων κοντά στο οποίο η δυναμική συμπεριφορά του πολυωνύμου (όταν επαναλαμβάνεται επανειλημμένα) αλλάζει δραστικά.

Βασικές ιδιότητες

Το σύνολο Μάντελμπροτ είναι ένα συμπαγές σύνολο, αφού είναι κλειστό και περιέχεται στον κλειστό δίσκο ακτίνας 2 γύρω από το αρχικό σημείο. Ένα σημείο $c$ ανήκει στο σύνολο Μάντελμπροτ αν και μόνο αν $|z_{n}|\leq 2$ για όλα τα $n\geq 0$. Με άλλα λόγια, η απόλυτη τιμή του $z_{n}$ πρέπει να παραμένει μικρότερη ή ίση με 2 για να ανήκει το $c$ στο σύνολο Μάντελμπροτ, $M$, και αν αυτή η απόλυτη τιμή υπερβαίνει το 2, η ακολουθία δραπετεύει στο άπειρο. Αφού $c=z_{1}$, προκύπτει ότι $|c|\leq 2$, διαπιστώνοντας ότι το $c$ θα βρίσκεται πάντα στον κλειστό δίσκο ακτίνας 2 γύρω από το αρχικό σημείο.

Η τομή του $M$ με τον πραγματικό άξονα είναι το διάστημα $[-2,{\frac {1}{4}}]$. Οι παράμετροι αυτού του διαστήματος μπορούν να τεθούν σε μία προς μία αντιστοιχία με εκείνες της πραγματικής λογιστικής οικογένειας,

$x_{n+1}=rx_{n}(1-x_{n}),\quad r\in [1,4].$

Η αντιστοιχία δίνεται από

$z=r\left({\frac {1}{2}}-x\right),\quad c={\frac {r}{2}}\left(1-{\frac {r}{2}}\right).$

Με αυτόν τον τρόπο, επιτυγχάνουμε μια αντιστοιχία μεταξύ ολόκληρου του χώρου παραμέτρων της λογιστικής οικογένειας και του συνόλου Μάντελμπροτ.

Οι Ντουάντι και Χάμπαρντ έδειξαν ότι το σύνολο Μάντελμπροτ είναι συνδεδεμένο. Κατασκεύασαν έναν ρητό σύμμορφο ισομορφισμό μεταξύ του συμπληρώματος του συνόλου Μάντελμπροτ και του συμπληρώματος του κλειστού μοναδιαίου δίσκου. Ο Μάντελμπροτ υπέθεσε αρχικά ότι το σύνολο Μάντελμπροτ ήταν ασύνδετο. Η εικασία αυτή βασίστηκε σε εικόνες υπολογιστή που παρήχθησαν από προγράμματα που δεν ήταν σε θέση να ανιχνεύσουν τα λεπτά νήματα που συνδέουν τα διάφορα μέρη του $M$ Μετά από περαιτέρω πειράματα, αναθεώρησε την εικασία του, αποφασίζοντας ότι το $M$ πρέπει να είναι συνδεδεμένο. Μια τοπολογική απόδειξη της συνδεσιμότητας ανακαλύφθηκε το 2001 από τον Τζέρεμι Καν . Εξωτερικές ακτίνες των κυμάτων κοντά στην ήπειρο περιόδου 1 στο σύνολο Μάντελμπροτ

Ο δυναμικός τύπος για την ομοιομορφία του συμπληρώματος του συνόλου Μάντελμπροτ, ο οποίος προκύπτει από την απόδειξη των Ντουάντι και Χάμπαρντ για τη συνδεσιμότητα του $M$ , οδηγεί σε εξωτερικές ακτίνες του συνόλου Μάντελμπροτ. Αυτές οι ακτίνες μπορούν να χρησιμοποιηθούν για τη μελέτη του συνόλου Μάντελμπροτ με συνδυαστικούς όρους και αποτελούν τη ραχοκοκαλιά του παραπαζλ Yoccoz.

Το όριο του συνόλου Μάντελμπροτ είναι το σημείο διακλάδωσης της οικογένειας των τετραγωνικών πολυωνύμων. Συγκεκριμένα, το όριο του συνόλου Μάντελμπροτ είναι το σύνολο όλων των παραμέτρων $c$ για τις οποίες η δυναμική του τετραγωνικού χάρτη $z_{n}=z_{n-1}^{2}+c$ παρουσιάζει ευαίσθητη εξάρτηση από τα $c,$ δηλαδή μεταβάλλεται απότομα υπό την επίδραση αυθαίρετων μικρών μεταβολών του $c.$. Μπορεί να οριστεί ως το σημείο διακλάδωσης της οικογένειας των τετραγωνικών πολυωνύμων. Μπορεί να κατασκευαστεί ως το οριακό σύνολο μιας ακολουθίας επίπεδων αλγεβρικών καμπυλών, των καμπυλών Μάντελμπροτ, του γενικού τύπου που είναι γνωστές ως πολυωνυμικές λεμνιστικές καμπύλες. Οι καμπύλες Μάντελμπροτ ορίζονται θέτοντας $p_{0}=z,\ p_{n+1}=p_{n}^{2}+z$, και στη συνέχεια ερμηνεύοντας το σύνολο των σημείων $|p_{n}(z)|=2$ στο μιγαδικό επίπεδο ως καμπύλη στο πραγματικό καρτεσιανό επίπεδο βαθμού $2^{n+1}$in x και y. Κάθε καμπύλη $n>0$ είναι η απεικόνιση ενός αρχικού κύκλου ακτίνας 2 υπό $p_{n}$. Αυτές οι αλγεβρικές καμπύλες εμφανίζονται στις εικόνες του συνόλου Μάντελμπροτ που υπολογίζονται χρησιμοποιώντας τον "αλγόριθμο του χρόνου διαφυγής" που αναφέρεται παρακάτω.

Μεταβολή της μέγιστης τιμής επανάληψης (40-300) στο σημείο -0,067 836 112 642 258 32 + 0,661 746 039 125 054 6 i του συνόλου Μάντελμπροτ.

Άλλες ιδιότητες

Περίοδοι των υπερβολικών συνιστωσών

Η κύρια καρδιοειδής καμπύλη είναι ο χώρος της περιόδου 1. Πρόκειται για την περιοχή των παραμέτρων $c$ για την οποία ο χάρτης

$f_{c}(z)=z^{2}+c$

διαθέτει ένα ελκυστικό σταθερό σημείο. Αποτελείται από όλες τις παραμέτρους της μορφής

$c(\mu ):={\frac {\mu }{2}}\left(1-{\frac {\mu }{2}}\right)$

για κάθε $\mu$ στον ανοικτό μοναδιαίο δίσκο. Στα αριστερά της κύριας καρδιοειδούς, προσαρτημένη σε αυτήν στο σημείο $c=-3/4$, είναι ορατός ένας κυκλικός βολβός, ο βολβός περιόδου 2. Ο βολβός αποτελείται από $c$για τα οποία η $f_{c}$ έχει κύκλο έλξης περιόδου 2. Πρόκειται για τον γεμάτο κύκλο ακτίνας 1/4 με κέντρο το -1.

Γενικότερα, για κάθε θετικό ακέραιο $q>2$ υπάρχουν $\phi (q)$κυκλικοί βολβοί εφαπτόμενοι στην κύρια καρδιοειδή που ονομάζονται βολβοί περιόδου q (όπου $\phi$ δηλώνει τη συνάρτηση φ του 'Οιλερ), οι οποίοι αποτελούνται από τις παραμέτρους $c$ για τις οποίες η $f_{c}$ έχει κύκλο έλξης περιόδου $q$. Πιο συγκεκριμένα, για κάθε πρωταρχική ρίζα $q$th της μονάδας $r=e^{2\pi i{\frac {p}{q}}}$ (όπου $0<{\frac {p}{q}}<1$), υπάρχει ένας βολβός περιόδου q που ονομάζεται ${\frac {p}{q}}$, ο οποίος εφάπτεται στην κύρια καρδιοειδή στην παράμετρο

$c_{\frac {p}{q}}:=c(r)={\frac {r}{2}}\left(1-{\frac {r}{2}}\right),$

Ο ελκτικός κύκλος στο 2/5-bulb απεικονίζεται πάνω στο σύνολο Τζούλια ("κινούμενη εικόνα")

και η οποία περιέχει παραμέτρους με $q$-κύκλους που έχουν συνδυαστικό αριθμό περιστροφής${\frac {p}{q}}$. Πιο συγκεκριμένα, οι $q$ περιοδικές συνιστώσες του Φατού που περιέχουν τον ελκυστικό κύκλο αγγίζουν όλες η μία την άλλη σε ένα κοινό σημείο (που συνήθως ονομάζεται σημείο $\alpha$). Αν ονομάσουμε αυτές τις συνιστώσες $U_{0},\dots ,U_{q-1}$ αριστερόστροφα, τότε η $f_{c}$ αντιστοιχίζει τη συνιστώσα $U_{j}$ στη συνιστώσα $U_{j+p\,(\operatorname {mod} q)}$.

Ελκυόμενοι κύκλοι και σύνολα Τζούλια για παραμέτρους στους λαμπτήρες 1/2, 3/7, 2/5, 1/3, 1/4 και 1/5

Η αλλαγή της συμπεριφοράς που συμβαίνει στο $c_{\frac {p}{q}}$ είναι γνωστή ως διακλάδωση: το ελκτικό σταθερό σημείο "συγκρούεται" με έναν απωθητικό κύκλο περιόδου-q. Καθώς περνάμε μέσα από την παράμετρο της διχοτόμησης στη σφαίρα${\tfrac {p}{q}}$, το ελκτικό σταθερό σημείο μετατρέπεται σε απωθητικό σταθερό σημείο (το $\alpha$ -σταθερό σημείο) και ο κύκλος περιόδου-q γίνεται ελκτικός.

Υπερβολικά στοιχεία

Οι βολβοί που είναι εσωτερικές συνιστώσες του συνόλου Μάντελμπροτ στις οποίες οι χάρτες $f_{c}$ έχουν έναν ελκυστικό περιοδικό κύκλο ονομάζονται υπερβολικές συνιστώσες.

Εικάζεται ότι αυτές είναι οι μόνες εσωτερικές περιοχές του $M$ και ότι είναι πυκνές στο $M$. Αυτό το πρόβλημα, γνωστό ως πυκνότητα υπερβολικότητας, είναι ένα από τα σημαντικότερα ανοιχτά προβλήματα της μιγαδικής δυναμικής. Οι υποθετικές μη υπερβολικές συνιστώσες του συνόλου Μάντελμπροτ συχνά ονομάζονται "queer" ή συνιστώσες-φάντασμα . Για πραγματικά τετραγωνικά πολυώνυμα, το ζήτημα αυτό αποδείχθηκε τη δεκαετία του 1990, ανεξάρτητα από τον Λιούμπιτς και από τους Γκράτσικ και Σβιόντεκ. (Σημειώστε ότι οι υπερβολικές συνιστώσες που τέμνουν τον πραγματικό άξονα αντιστοιχούν ακριβώς σε περιοδικά παράθυρα στο διάγραμμα Φάιγκενμπαουμ. Το αποτέλεσμα αυτό δείχνει επομένως ότι τέτοια παράθυρα υπάρχουν κοντά σε κάθε παράμετρο του διαγράμματος).

Δεν μπορούν να προσεγγιστούν όλες οι υπερβολικές συνιστώσες με μια ακολουθία άμεσων διακλαδώσεων από το κύριο καρδιοειδές του συνόλου Μάντελμπροτ. Μια τέτοια συνιστώσα μπορεί να επιτευχθεί με μια ακολουθία άμεσων διακλαδώσεων από την κύρια καρδιοειδή ενός μικρού αντιγράφου του Μάντελμπροτ (βλ. παρακάτω).

Κάθε μία από τις υπερβολικές συνιστώσες διαθέτει ένα κέντρο, το οποίο είναι ένα σημείο c τέτοιο ώστε η εσωτερική περιοχή Φατού για την $f_{c}(z)$ να έχει έναν υπερ-ελκυστικό κύκλο - δηλαδή η έλξη να είναι άπειρη. Αυτό σημαίνει ότι ο κύκλος περιέχει το κρίσιμο σημείο 0, έτσι ώστε το 0 να επιστρέφει στον εαυτό του μετά από μερικές επαναλήψεις. Επομένως, $f_{c}^{n}(0)=0$ για κάποιο n. Αν ονομάσουμε αυτό το πολυώνυμο $Q^{n}(c)$ (αφήνοντάς το να εξαρτάται από το c αντί του z), έχουμε ότι $Q^{n+1}(c)=Q^{n}(c)^{2}+c$ και ότι ο βαθμός του $Q^{n}(c)$ is $2^{n-1}$. Συνεπώς, η κατασκευή των κέντρων των υπερβολικών συνιστωσών είναι δυνατή με τη διαδοχική επίλυση των εξισώσεων $Q^{n}(c)=0,n=1,2,3,...$ Ο αριθμός των νέων κέντρων που παράγονται σε κάθε βήμα δίνεται από το OEIS του Sloane: A000740.

Τοπική συνδεσιμότητα

Εικάζεται ότι το σύνολο Μάντελμπροτ είναι τοπικά συνδεδεμένο. Αυτή η εικασία είναι γνωστή ως MLC (για το Μάντελμπροτ τοπικά συνδεδεμένο). Με την εργασία των Αντριέν Ντουαντί και Τζον Χ. Χάμπαρντ, αυτή η εικασία θα οδηγούσε σε ένα απλό αφηρημένο μοντέλο "τσιμπημένου δίσκου" του συνόλου Μάντελμπροτ. Ειδικότερα, θα συνεπαγόταν τη σημαντική εικασία της υπερβολικότητας που αναφέρθηκε παραπάνω.

Το έργο του Ζαν-Κριστόφ Γιοκόζ καθιέρωσε την τοπική συνδεσιμότητα του συνόλου Μάντελμπροτ σε όλες τις πεπερασμένα επανακανονικοποιήσιμες παραμέτρους, δηλαδή, χονδρικά μιλώντας, σε εκείνες που περιέχονται μόνο σε πεπερασμένα πολλά μικρά αντίγραφα Μάντελμπροτ Από τότε, η τοπική συνδεσιμότητα έχει αποδειχθεί σε πολλά άλλα σημεία του $M$, αλλά η πλήρης εικασία είναι ακόμα ανοιχτή.

Αυτο-ομοιότητα

Η αυτο-ομοιότητα στο σύνολο Μάντελμπροτ απεικονίζεται με μεγέθυνση σε ένα στρογγυλό στοιχείο ενώ η σάρωση γίνεται προς την αρνητική κατεύθυνση x. Το κέντρο της οθόνης μετακινείται προς τα αριστερά, από το πέμπτο στο έβδομο στρογγυλό στοιχείο (-1,4002, 0) στο (-1,4011, 0), ενώ η προβολή μεγεθύνεται κατά έναν παράγοντα 21,78 για να προσεγγίσει το τετράγωνο του λόγου Φάιγκενμπαουμ

Αυτο-ομοιότητα στο σύνολο Μάντελμπροτ που παρουσιάζεται με μεγέθυνση σε ένα στρογγυλό χαρακτηριστικό ενώ η σάρωση γίνεται προς την αρνητική κατεύθυνση x. Το κέντρο της οθόνης μετακινείται αριστερά από το πέμπτο στο έβδομο στρογγυλό χαρακτηριστικό (-1,4002, 0) έως (-1,4011, 0) ενώ η προβολή μεγεθύνεται κατά έναν παράγοντα 21,78 για να προσεγγίσει το τετράγωνο του λόγου Φάιγκενμπαουμ.

Το σύνολο Μάντελμπροτ είναι αυτο-ομοειδές υπό μεγέθυνση στις γειτονιές των σημείων Μισιούρεβιτς. Εικάζεται επίσης ότι είναι αυτο-ομοειδές γύρω από τα γενικευμένα σημεία Φεϊγκενμπάουμ (π.χ. -1,401155 ή -0,1528 + 1,0397i), με την έννοια ότι συγκλίνει σε ένα οριακό σύνολο. Το σύνολο Μάντελμπροτ είναι γενικά οιονεί αυτο-ομοειδές, καθώς μπορούν να βρεθούν μικρές ελαφρώς διαφορετικές εκδοχές του εαυτού του σε αυθαίρετα μικρές κλίμακες. Αυτά τα αντίγραφα του συνόλου Μάντελμπροτ είναι όλα ελαφρώς διαφορετικά, κυρίως λόγω των λεπτών νημάτων που τα συνδέουν με το κύριο σώμα του συνόλου.

Άλλα αποτελέσματα

Η διάσταση Χάουστορφ του συνόλου Μάντελμπροτ είναι ίση με 2, σύμφωνα με ένα αποτέλεσμα του Μιτσουχίρο Σισικούρα. Το γεγονός ότι αυτή η διάσταση είναι κατά έναν ακέραιο μεγαλύτερο από την τοπολογική διάσταση, η οποία είναι 1, αντικατοπτρίζει τη φράκταλ φύση του συνόλου Μάντελμπροτ. Το αποτέλεσμα του Σισικούρα δείχνει ότι το όριο του συνόλου Μάντελμπροτ είναι "κυματιστό"- γεμίζει τοπικά τον χώρο τόσο αποτελεσματικά όσο μια δισδιάστατη επίπεδη περιοχή. Επομένως, είναι πιθανό το όριο του συνόλου Μάντελμπροτ, αν και καμπύλη, να έχει μη μηδενικό εμβαδόν (ή, πιο επίσημα, να έχει θετικό επίπεδο μέτρο Λεμπέσκε). Το ερώτημα αν αυτό ισχύει στην πραγματικότητα παραμένει ανοιχτό.

Έχει αποδειχθεί ότι το γενικευμένο σύνολο Μάντελμπροτ σε χώρους υψηλότερων διαστάσεων υπερσύμπλοκων αριθμών (δηλαδή όταν η δύναμη $\alpha$ της επαναλαμβανόμενης μεταβλητής $z$ τείνει στο άπειρο) συγκλίνει στη μοναδιαία σφαίρα ($\alpha$-1).

Στο μοντέλο Μπλουμ-Σουμπ-Σμαλ του πραγματικού υπολογισμού, το σύνολο Μάντελμπροτ δεν είναι υπολογίσιμο, αλλά το συμπλήρωμα του είναι υπολογίσιμο. Πολλά απλά αντικείμενα (π.χ. το γράφημα εκθετικοποίησης) δεν είναι υπολογίσιμα ούτε στο μοντέλο BSS. Προς το παρόν, δεν είναι γνωστό αν το σύνολο Μάντελμπροτ είναι υπολογίσιμο στα μοντέλα πραγματικών υπολογισμών που βασίζονται στην υπολογίσιμη ανάλυση, τα οποία αντιστοιχούν περισσότερο στη διαισθητική έννοια της "ανίχνευσης του συνόλου από έναν υπολογιστή". Ο Χέρτλινγκ έδειξε ότι το σύνολο Μάντελμπροτ είναι υπολογίσιμο σε αυτό το μοντέλο, αν η εικασία της υπερβολικότητας είναι αληθής.

Σχέση με τα σύνολα Τζούλια (Julia)

Ως συνέπεια του ορισμού του συνόλου Μάντελμπροτ, υπάρχει στενή αντιστοιχία μεταξύ της γεωμετρίας του συνόλου Μάντελμπροτ σε ένα δεδομένο σημείο και της δομής του αντίστοιχου συνόλου Julia. Παραδείγματος χάριν, μια τιμή του c ανήκει στο σύνολο Μάντελμπροτ αν το αντίστοιχο σύνολο Julia είναι συνδεδεμένο. Το σύνολο Μάντελμπροτ μπορεί επομένως να θεωρηθεί ως ένας χάρτης συνδεδεμένων συνόλων Τζούλια. Αυτή η αρχή αξιοποιείται σε όλα σχεδόν τα βαθιά αποτελέσματα για το σύνολο Μάντελμπροτ. Για παράδειγμα, ο Σισικούρα απέδειξε ότι, για ένα πυκνό σύνολο παραμέτρων στο όριο του συνόλου Μάντελμπροτ, το σύνολο Τζούλια έχει διάσταση Χάουστορφ δύο, και στη συνέχεια μετέφερε αυτή την πληροφορία στο επίπεδο παραμέτρων. Ομοίως, ο Γιόκοζ απέδειξε πρώτα την τοπική συνδεσιμότητα των συνόλων Τζούλια, πριν την καθιερώσει για το σύνολο Μάντελμπροτ με τις αντίστοιχες παραμέτρους..

Γεωμετρία

Για κάθε ρητό αριθμό ${\tfrac {p}{q}}$, όπου τα p και q είναι σχετικά πρώτοι, μια υπερβολική συνιστώσα περιόδου q διχάζεται από την κύρια καρδιοειδή σε ένα σημείο στην άκρη της καρδιοειδούς που αντιστοιχεί σε εσωτερική γωνία ${\tfrac {2\pi p}{q}}$ . Το τμήμα του συνόλου Μάντελμπροτ που συνδέεται με την κύρια καρδιοειδή σε αυτό το σημείο διακλάδωσης ονομάζεται άκρο p/q-limb. Πειράματα σε υπολογιστές δείχνουν ότι η διάμετρος του άκρου τείνει στο μηδέν καθώς ${\tfrac {1}{q^{2}}}$. Η πιο γνωστή τρέχουσα εκτίμηση είναι η ποιότητα Yoccoz-ine, η οποία δείχνει ότι το μέγεθος τείνει στο μηδέν ως ${\tfrac {1}{q}}$

Ένα άκρο με περίοδο q limb θα έχει $q-1$"κεραίες" στην κορυφή του άκρου του. Η περίοδος ενός συγκεκριμένου βολβού προσδιορίζεται με την καταμέτρηση αυτών των κεραιών. Ο αριθμητής του αριθμού των περιστροφών, p, προκύπτει από την αρίθμηση κάθε κεραίας αριστερόστροφα από το σκέλος, από 1 έως $q-1$, και τον προσδιορισμό της μικρότερης κεραίας

Το π στο σύνολο Μάντελμπροτ

Σε μια προσπάθεια να αποδείξει ότι το πάχος του μέλους p/qείναι μηδέν, ο Ντέιβιντ Μπολ πραγματοποίησε ένα πείραμα σε υπολογιστή το 1991 στο οποίο υπολόγισε τον αριθμό των επαναλήψεων που απαιτούνται για να αποκλίνει η σειρά για $z=-{\tfrac {3}{4}}+i\varepsilon$ ($-{\tfrac {3}{4}}$ που είναι η θέση του). Δεδομένου ότι η σειρά δεν αποκλίνει για την ακριβή τιμή $z=-{\tfrac {3}{4}}$, ο αριθμός των απαιτούμενων επαναλήψεων αυξάνεται με ένα μικρό $\varepsilon$. Αποδεικνύεται ότι ο πολλαπλασιασμός της τιμής του $\varepsilon$ με τον αριθμό των απαιτούμενων επαναλήψεων δίνει μια προσέγγιση του $\pi$ η οποία γίνεται καλύτερη για μικρότερα $\varepsilon$. Παραδείγματος χάριν, για $\varepsilon$ = 0,0000001, ο αριθμός των επαναλήψεων είναι 31415928 και το γινόμενο είναι 3,1415928. Το 2001, ο Άαρον Κλεμπάνοφ απέδειξε την ανακάλυψη του Μπολ.

Ακολουθία Φιμπονάτσι στο σύνολο Μάντελμπροτ

Μπορεί να αποδειχθεί ότι η ακολουθία Φιμπονάτσι βρίσκεται μέσα στο σύνολο Μάντελμπροτ και ότι υπάρχει σχέση μεταξύ του κύριου καρδιοειδούς και του διαγράμματος Φάρεϊ . Με την απεικόνιση του κύριου καρδιοειδούς σε ένα δίσκο, η ποσότητα των κεραιών που εκτείνεται από την αμέσως μεγαλύτερη υπερβολική συνιστώσα και η οποία βρίσκεται μεταξύ των δύο προηγουμένως επιλεγμένων συνιστωσών, αντιστοιχεί στην ακολουθία Φιμπονάτσι. Ο αριθμός των κεραιών συσχετίζεται επίσης με το διάγραμμα Φάρεϊ και τα ποσά του παρονομαστή στις αντίστοιχες κλασματικές τιμές, οι οποίες σχετίζονται με την απόσταση γύρω από το δίσκο. Τα δύο μέρη αυτών των κλασματικών τιμών μπορούν να προστεθούν μαζί μετά το ${\frac {1}{3}}$ για να προκύψει η θέση της επόμενης υπερβολικής συνιστώσας στην ακολουθία. Έτσι, η ακολουθία Φιμπονάτσι των 1, 2, 3, 5, 8, 13 και 21 βρίσκεται στο σύνολο Μάντελμπροτ.

Έκθεση εικόνων

Τα όρια του συνόλου Μάντελμπροτ παρουσιάζουν πιο περίπλοκες λεπτομέρειες όσο πιο κοντά κοιτάζει κανείς ή μεγεθύνει την εικόνα. Ακολουθεί ένα παράδειγμα μιας ακολουθίας εικόνας που μεγεθύνεται σε μια επιλεγμένη τιμή c.

Η μεγέθυνση της τελευταίας εικόνας σε σχέση με την πρώτη είναι περίπου 10¹⁰ προς 1. Σχετικά με μια συνηθισμένη οθόνη υπολογιστή, αναπαριστά ένα τμήμα ενός συνόλου Μάντελμπροτ με διάμετρο 4 εκατομμυρίων χιλιομέτρων.

• 
  Έναρξη. Σύνολο Μάντελμπροτ με διαρκώς χρωματισμένο περιβάλλον.
• 
  Ο χώρος μεταξύ του "κεφαλιού" και του "σώματος", γνωστός και ως "ιπποκάμπειος κοιλάδα"."
• 
  Διπλές σπείρες στα αριστερά, "ιππόκαμποι" στα δεξιά
• 
  "ιππόκαμπος" ανάποδα

Το "σώμα" του ιππόκαμπου αποτελείται από 25 "ακτίνες", δηλαδή δύο ομάδες των 12 "ακτίνων" η καθεμία και μία "ακτίνα" που συνδέεται με την κύρια καρδιοειδή. Αυτές οι δύο ομάδες μπορούν να αποδοθούν με μεταμόρφωση στα δύο "δάχτυλα" του "άνω χεριού" του συνόλου Μάντελμπροτ- έτσι, ο αριθμός των "ακτίνων" αυξάνεται κατά 2 από τον έναν "ιππόκαμπο" στον επόμενο- ο "κόμβος" είναι ένα σημείο Μισιούρεβιτς. Μεταξύ του "άνω σώματος" και της "ουράς", υπάρχει ένα παραμορφωμένο αντίγραφο του συνόλου Μάντελμπροτ, που ονομάζεται "δορυφόρος".

• 
  Το κεντρικό άκρο της "ουράς του ιππόκαμπου" είναι επίσης σημείο Μισιούρεβιτς..
• 
  Μέρος της "ουράς" - υπάρχει μόνο ένα μονοπάτι από λεπτές δομές που διασχίζει ολόκληρη την "ουρά". Αυτό το τεθλασμένο μονοπάτι περνάει μέσα από τις "κόμβους" των μεγάλων αντικειμένων με 25 "ακτίνες" μέσα και έξω από την "ουρά"- το σύνολο Μάντελμπροτ είναι επομένως ένας απλά συνδεδεμένος χώρος, πράγμα που σημαίνει ότι δεν υπάρχουν νησιά ή δρόμοι βρόχων γύρω από μια τρύπα.
• 
  Δορυφόρος. Οι δύο "ουρές ιππόκαμπου" είναι η αρχή μιας σειράς ομόκεντρων στεφανιών με τον δορυφόρο στο κέντρο.
• 
  Κάθε μια από αυτές τις κορώνες αποτελείται από παρόμοιες "ουρές ιππόκαμπου", ο αριθμός των οποίων αυξάνεται με δυνάμεις του 2, ένα τυπικό φαινόμενο στο περιβάλλον των δορυφόρων. Η μοναδική διαδρομή προς το σπειροειδές κέντρο περνάει τον δορυφόρο από την αύλακα του καρδιοειδούς στην κορυφή της "κεραίας" στην "κεφαλή".
• 
  "Κεραία" του δορυφόρου. Υπάρχουν αρκετοί δορυφόροι δεύτερης τάξης.
• 
  Η "κοιλάδα του ιππόκαμπου" του δορυφόρου. Όλες οι δομές από την αρχή επανεμφανίζονται.
• 
  Διπλές σπείρες και "ιππόκαμποι" - σε αντίθεση με τη δεύτερη εικόνα από την αρχή, έχουν προσαρτήματα που αποτελούνται από δομές όπως "ουρές ιππόκαμπων"- αυτό δείχνει την τυπική σύνδεση n + 1 διαφορετικών δομών στο περιβάλλον δορυφόρων της τάξης n, εδώ για την απλούστερη περίπτωση n = 1.
• 
  Διπλές σπείρες με δορυφόρους δεύτερης τάξης - κατ' αναλογία με τους "ιππόκαμπους", οι διπλές σπείρες μπορούν να ερμηνευθούν ως μεταμόρφωση της "κεραίας".
• 
  Στο έξω μέρος των προσαρτημάτων, μπορούν να αναγνωριστούν νησίδες δομών- έχουν σχήμα σαν το J_c του συνόλου Julia- το μεγαλύτερο από αυτά μπορεί να βρεθεί στο κέντρο του "διπλού γάντζου" στη δεξιά πλευρά.
• 
  Μέρος του "διπλού γάντζου".
• 
  Νησιά.
• 
  Λεπτομέρεια ενός νησιού.
• 
  Λεπτομέρεια του σπιράλ.

Τα νησιά στο προτελευταίο στάδιο φαίνεται να αποτελούνται από άπειρα μέρη, όπως συμβαίνει με το αντίστοιχο σύνολο Τζούλια $J_{c}$. Συνδέονται με μικροσκοπικές δομές, έτσι ώστε το σύνολο να αντιπροσωπεύει ένα απλά συνδεδεμένο σύνολο. Οι μικροσκοπικές δομές συναντώνται σε έναν δορυφόρο στο κέντρο, ο οποίος είναι πολύ μικρός για να αναγνωριστεί σε αυτή τη μεγέθυνση. Η τιμή του $c$ για το αντίστοιχο $J_{c}$ δεν είναι το κέντρο της εικόνας αλλά, σε σχέση με το κύριο σώμα του συνόλου Μάντελμπροτ, έχει την ίδια θέση με το κέντρο αυτής της εικόνας σε σχέση με τον δορυφόρο που φαίνεται στο βήμα 6.

Εσωτερική δομή

Ενώ το σύνολο Μάντελμπροτ αναπαρίσταται συνήθως με την παρουσίαση των λεπτομερειών των εξωτερικών ορίων, η δομή του οριοθετημένου συνόλου μπορεί επίσης να αποκαλυφθεί. Παραδείγματος χάριν, υπολογίζοντας αν μια δεδομένη τιμή c είναι δεσμευμένη ή όχι, εφόσον παραμένει δεσμευμένη, η μέγιστη τιμή που επιτυγχάνεται από τον αριθμό αυτό μπορεί να συγκριθεί με την τιμή c στο συγκεκριμένο σημείο. Αν χρησιμοποιηθεί η μέθοδος του αθροίσματος των τετραγώνων, ο αριθμός που θα υπολογιστεί θα είναι max : (real^2 + imaginary^2) - c:(real^2 + imaginary^2). Το μέγεθος αυτού του υπολογισμού μπορεί να αναπαρασταθεί ως μια τιμή σε μια κλίση.

Αυτό παράγει αποτελέσματα όπως τα παρακάτω, κλίσεις με ευδιάκριτα άκρα και περιγράμματα καθώς πλησιάζετε τα όρια. Οι κινούμενες εικόνες χρησιμοποιούνται για να αναδείξουν τα όρια της διαβάθμισης.

• 
  Κινούμενη δομή κλίσης μέσα στο σύνολο Μάντελμπροτ
• 
  Κινούμενη δομή κλίσης μέσα στο σύνολο Μάντελμπροτ, λεπτομέρεια
• 
  Απεικόνιση προοδευτικών επαναλήψεων από 285 έως περίπου 200.000 με αντίστοιχες οριοθετημένες κλίσεις με κινούμενες εικόνες
• 
  Μικρογραφία για κλίση με προοδευτικές επαναλήψεις

Γενικεύσεις

Κινούμενες εικόνες του συνόλου Multibrot για d από 0 έως 5 (αριστερά) και από 0,05 έως 2 (δεξιά).

Ένα 4D σύνολο Τζούλια μπορεί να προβάλλεται ή να διασταυρώνεται σε 3D, και λόγω αυτού είναι επίσης δυνατό να δημιουργηθεί ένα 4D σύνολο Μάντελμπροτ.

Multibrot σύνολα

Τα σύνολα Multibrot είναι οριοθετημένα σύνολα που βρίσκονται στο μιγαδικό επίπεδο για μέλη της γενικής μονικής μονοπαραγοντικής πολυωνυμικής οικογένειας αναδρομών

$z\mapsto z^{d}+c$.

Για έναν ακέραιο αριθμό d, αυτά τα σύνολα είναι τόποι συνδεσιμότητας για σύνολα Τζούλια που κατασκευάζονται από τον ίδιο τύπο. Ο πλήρης κυβικός τόπος συνδεσιμότητας μελετήθηκε επίσης- εδώ εξετάζουμε την αναδρομή δύο παραμέτρων $z\mapsto z^{3}+3kz+c$, της οποίας τα δύο κρίσιμα σημεία είναι οι μιγαδικές τετραγωνικές ρίζες της παραμέτρου k. Μια παράμετρος βρίσκεται στον τόπο κυβικής συνδεσιμότητας αν τα δύο κρίσιμα σημεία είναι σταθερά. Για γενικές οικογένειες ολομορφικών συναρτήσεων, το όριο του συνόλου Μάντελμπροτ γενικεύεται στον τόπο διακλάδωσης.

Το σύνολο Multibrot προκύπτει μεταβάλλοντας την τιμή του εκθέτη d. Το άρθρο περιέχει ένα βίντεο που δείχνει την εξέλιξη από d = 0 έως 7, οπότε υπάρχουν 6, δηλαδή $(d-1)$ λοβοί γύρω από την περίμετρο. Γενικά, όταν το d είναι ένας θετικός ακέραιος, η κεντρική περιοχή κάθε ενός από αυτά τα σύνολα είναι πάντα ένα επικόμβιο από $(d-1)$ λοβούς. Μια παρόμοια εξέλιξη με αρνητικούς ακέραιους εκθέτες οδηγεί σε $(1-d)$ υποδοχές μέσα σε ένα δακτύλιο, όπου η κύρια κεντρική περιοχή του συνόλου είναι μια υποκυκλοειδής από $(1-d)$ ακρολοφίες.

Υψηλότερες διαστάσεις

Δεν υπάρχει τέλεια επέκταση του συνόλου Μάντελμπροτ σε 3D, επειδή δεν υπάρχει τρισδιάστατο ανάλογο των μιγαδικών αριθμών στο οποίο να μπορεί να επαναληφθεί. Υπάρχει μια επέκταση των μιγαδικών αριθμών σε 4 διαστάσεις, τα κουατερνιόνια, η οποία δημιουργεί μια ιδανική επέκταση του συνόλου Μάντελμπροτ και των συνόλων Τζούλια σε 4 διαστάσεις, τα οποία μπορούν στη συνέχεια να κοπούν ή να προβληθούν σε μια τρισδιάστατη δομή. Το σύνολο Μάντελμπροτ των κουατερνιόνων (4 διαστάσεις) είναι απλώς ένα στερεό της περιστροφής του συνόλου Μάντελμπροτ σε 2 διαστάσεις (στο επίπεδο j-k), και επομένως δεν είναι ενδιαφέρον να το δούμε. Αν πάρουμε μια τομή σε 3 διαστάσεις στο $d=0\ (q=a+bi+cj+dk)$ παίρνουμε ένα στερεό της περιστροφής του συνόλου Μάντελμπροτ σε 2 διαστάσεις γύρω από τον πραγματικό άξονα.

Άλλες μη αναλυτικές απεικονίσεις

Εικόνα του φράκταλ Tricorn/Mandelbar

Ιδιαίτερο ενδιαφέρον παρουσιάζει το φράκταλ του τρικέρατου, ο τόπος συνδεσιμότητας της αντι-ολομορφικής οικογένειας

$z\mapsto {\bar {z}}^{2}+c$.

Το τρικέρατο (που μερικές φορές ονομάζεται επίσης Mandelbar) εντοπίστηκε από τον Milnor στη μελέτη του για τις παραμετρικές φέτες των πραγματικών κυβικών πολυωνύμων. Δεν είναι τοπικά συνδεδεμένο. Η ιδιότητα αυτή κληρονομείται από τον τόπο συνδεσιμότητας των πραγματικών κυβικών πολυωνύμων.

Μια άλλη μη αναλυτική γενίκευση είναι το φράκταλ του φλεγόμενου πλοίου (Burning Ship), το οποίο λαμβάνεται με την επανάληψη των παρακάτω:

$z\mapsto (|\Re \left(z\right)|+i|\Im \left(z\right)|)^{2}+c$.

Σχέδια σε υπολογιστή

Υπάρχουν πολλοί διαφορετικοί αλγόριθμοι για την απεικόνιση του συνόλου Μάντελμπροτ με τη χρήση υπολογιστή. Εδώ προτείνεται ο πιο διαδεδομένος και απλούστερος αλγόριθμος, δηλαδή ο αφελής αλγόριθμος "χρόνος διαρροής". Στον αλγόριθμο του χρόνου διαρροής, εκτελείται ένας επαναλαμβανόμενος υπολογισμός για κάθε σημείο x, y στην περιοχή σχεδίασης και, ανάλογα με τη συμπεριφορά αυτού του υπολογισμού, επιλέγεται ένα χρώμα για το συγκεκριμένο εικονοστοιχείο (pixel).

Οι θέσεις x και y κάθε σημείου χρησιμοποιούνται ως αρχικές τιμές σε έναν επαναλαμβανόμενο ή επαναληπτικό υπολογισμό (που περιγράφεται λεπτομερώς παρακάτω). Το αποτέλεσμα κάθε επανάληψης χρησιμοποιείται ως αρχικές τιμές για την επόμενη. Οι τιμές ελέγχονται σε κάθε επανάληψη για να διαπιστωθεί εάν έχουν φθάσει σε μια κρίσιμη κατάσταση "διαρροής" ή "διάσωσης". Εάν επιτευχθεί αυτή η συνθήκη, ο υπολογισμός σταματά, το εικονοστοιχείο σχεδιάζεται και εξετάζεται το επόμενο σημείο x, y.

Το χρώμα κάθε σημείου αντιπροσωπεύει πόσο γρήγορα οι τιμές έφτασαν στο σημείο διαφυγής. Συχνά, χρησιμοποιείται μαύρο χρώμα για να δείξει τις τιμές που αποτυγχάνουν να διαφύγουν πριν από το όριο επανάληψης και χρησιμοποιούνται προοδευτικά ανοιχτότερα χρώματα για τα σημεία που διαφεύγουν. Αυτό δίνει μια οπτική αναπαράσταση του αριθμού των κύκλων που απαιτούνται για την επίτευξη της συνθήκης διαφυγής.

Για την απόδοση μιας τέτοιας εικόνας, η περιοχή του μιγαδικού επιπέδου που εξετάζουμε υποδιαιρείται σε ορισμένο αριθμό εικονοστοιχείων. Για να χρωματίσουμε ένα από αυτά τα εικονοστοιχεία, ας συμβολίσουμε $c$ το μέσο του εικονοστοιχείου αυτού. Επαναλαμβάνουμε το κρίσιμο σημείο 0 κάτω από το$f_{c}$, ελέγχοντας σε κάθε βήμα αν το σημείο της τροχιάς έχει ακτίνα μεγαλύτερη από 2. Αν ναι, το$c$ δεν ανήκει στο σύνολο Μάντελμπροτ και χρωματίζουμε το εικονοστοιχείο ανάλογα με τον αριθμό των επαναλήψεων που χρησιμοποιήθηκαν για την ανακάλυψή του. Διαφορετικά, συνεχίζουμε την επανάληψη μέχρι να φτάσουμε σε έναν σταθερό αριθμό βημάτων, μετά από τον οποίο αποφασίζουμε ότι η παράμετρός μας βρίσκεται "πιθανώς" στο σύνολο Μάντελμπροτ, ή τουλάχιστον πολύ κοντά σε αυτό, και χρωματίζουμε το εικονοστοιχείο με μαύρο χρώμα.

Σε ψευδοκώδικα, αυτός ο αλγόριθμος θα έμοιαζε ως εξής. Ο αλγόριθμος δεν χρησιμοποιεί μιγαδικούς αριθμούς και προσομοιώνει χειροκίνητα τις πράξεις σε μιγαδικούς αριθμούς χρησιμοποιώντας δύο πραγματικούς αριθμούς, για όσους δεν έχουν μιγαδικό τύπο δεδομένων. Το πρόγραμμα μπορεί να απλοποιηθεί εάν η γλώσσα προγραμματισμού περιλαμβάνει πράξεις σύνθετου τύπου δεδομένων.

    για κάθε εικονοστοιχείο (Px, Py) στην οθόνη do
    x0 := scaled x coordinate of pixel (scaled to lie in the Mandelbrot X scale (-2.00, 0.47))
    y0 := scaled y coordinate of pixel (scaled to lie in the Mandelbrot Y scale (-1.12, 1.12))
    x := 0.0
    y := 0.0
    iteration := 0
    max_iteration := 1000
    while (x*x + y*y ≤ 2*2 AND iteration < max_iteration) do
        xtemp := x*x - y*y + x0
        y := 2*x*y + y0
        x := xtemp
        iteration := iteration + 1
    
    color := palette[iteration]
    plot(Px, Py, color)

Εδώ, σχετικά με τον ψευδοκώδικα για $c$, $z$ και $f_{c}$:

• $z=x+iy$
• $z^{2}=x^{2}+i2xy-y^{2}$
• $c=x_{0}+iy_{0}$

και έτσι, όπως φαίνεται και στον ψευδοκώδικα στον υπολογισμό των x και y:

• $x=\mathop {\mathrm {Re} } (z^{2}+c)=x^{2}-y^{2}+x_{0}$ και $y=\mathop {\mathrm {Im} } (z^{2}+c)=2xy+y_{0}$.

Για να έχουμε πολύχρωμες εικόνες του συνόλου, η ανάθεση ενός χρώματος σε κάθε τιμή του αριθμού των επαναλήψεων που εκτελούνται μπορεί να γίνει με τη χρήση μιας από τις διάφορες συναρτήσεις (γραμμική, εκθετική κ.λπ.).

Αναφορές στη δημόσια πολιτιστική ζωή

Το σύνολο Μάντελμπροτ θεωρείται το δημοφιλέστερο φράκταλ και αναφέρθηκε αρκετές φορές στη δημόσια πολιτιστική ζωή.

• Το τραγούδι του Τζόναθαν Κούλτον " Σύνολο Μαντελμπρότ" είναι ένας φόρος τιμής τόσο στο ίδιο το φράκταλ όσο και στον άνθρωπο από τον οποίο πήρε το όνομά του, τον Μπενουά Μαντελμπρότ.
• Πολλοί τίτλοι κομματιών στο ντεμπούτο άλμπουμ των Blue Man Group του 1999, Audio, αναφέρονται στο σύνολο Μάντελμπροτ. Αυτοί είναι οι τίτλοι "'Εναρξη Μάντελμπροτ", "Mandelgroove" και "'Κλάιν Μάντελμπροτ".
• Το δεύτερο βιβλίο της σειράς Mode του Piers Anthony, Φρακταλική Μόδα, περιγράφει έναν κόσμο που είναι ένα τέλειο τρισδιάστατο μοντέλο του συνόλου.
• Το μυθιστόρημα του Άρθουρ Κ. Κλαρκ "Το φάντασμα από τις μεγάλες όχθες" (The Ghost from the Grand Banks) περιλαμβάνει μια τεχνητή λίμνη που φτιάχτηκε για να αναπαράγει το σχήμα του συνόλου Μάντελμπροτ.
• Ο Μπενουά Μαντελμπρό και το ομώνυμο σύνολο αποτέλεσαν το θέμα του Google Doodle στις 20 Νοεμβρίου 2020 (96α γενέθλια του αείμνηστου Μπενουά Μαντελμπρό).
• Το αμερικανικό ροκ συγκρότημα Heart έχει μια εικόνα ενός συνόλου Μάντελμπροτ στο εξώφυλλο του άλμπουμ του 2004, Jupiters Darling.
• Το βρετανικό μπλακ μέταλ συγκρότημα Anaal Nathrakh χρησιμοποιεί μια εικόνα που μοιάζει με το σύνολο Mandelbrot στο εξώφυλλο του άλμπουμ τους Eschaton.
• Η τηλεοπτική σειρά Dirk Gently's Holistic Detective Agency (2016) παρουσιάζει σε περίοπτη θέση το σύνολο Μάντελμπροτ σε σχέση με τα οράματα του χαρακτήρα της Αμάντα. Στη δεύτερη σεζόν, το σακάκι της έχει μια μεγάλη εικόνα του φράκταλ στο πίσω μέρος.
• Στο βιβλίο του Ίαν Στιούαρτ Φλάτερλαντ του 2001, υπάρχει ένας χαρακτήρας που ονομάζεται Μαντελμπλότ, ο οποίος βοηθάει στην εξήγηση των φράκταλ στους χαρακτήρες και στον αναγνώστη.
• Η σειρά κόμικς του Άλαν Μουρ "Μεγάλοι αριθμοί", που δεν ολοκληρώθηκε το 1990, στηρίχθηκε στη μελέτη του Μάντελμπροτ σχετικά με τη γεωμετρία των φράκταλ και τη θεωρία του χάους για να στηρίξει τη δομή του έργου. Κάποια στιγμή ο Μουρ είχε σκοπό να ονομάσει τη σειρά κόμικς "Σύνολο Μάντελμπροτ".

Δείτε επίσης

• Σύνολο Julia
• Απολλώνιο πρόβλημα
• Απολλώνιος ο Περγαίος
• Σύνολο Κάντορ
• Τρικέρατο (μαθηματικά)

Δημοσιεύσεις

• Milnor, John W. (2006). Dynamics in One Complex Variable. Annals of Mathematics Studies. 160 (Third έκδοση). Princeton University Press. ISBN 0-691-12488-4. 
  (First appeared in 1990 as a Stony Brook IMS Preprint, available as arXiV:math.DS/9201272 )
• Lesmoir-Gordon, Nigel (2004). The Colours of Infinity: The Beauty, The Power and the Sense of Fractals. ISBN 1-904555-05-5. 
  (includes a DVD featuring Arthur C. Clarke and David Gilmour)
• Peitgen, Heinz-Otto· Jürgens, Hartmut· Saupe, Dietmar (2004) [1992]. Chaos and Fractals: New Frontiers of Science. New York: Springer. ISBN 0-387-20229-3. 

Εξωτερικοί σύνδεσμοι

• Chaos and Fractals στο Curlie
• Video: Mandelbrot fractal zoom to 6.066 e228
• Relatively simple explanation of the mathematical process, by Dr Holly Krieger, MIT
• Mandelbrot Viewer: Browser based Mandelbrot set renderer including a gallery with examples.
• Various algorithms for calculating the Mandelbrot set (on Rosetta Code)
• Fractal calculator written in Lua by Deyan Dobromiroiv, Sofia, Bulgaria