Καμπύλη Blancmange

Ένα διάγραμμα της καμπύλης blancmange.

Στα μαθηματικά, η καμπύλη blancmange είναι μια καμπύλη που κατασκευάζεται με υποδιαίρεση του μέσου σημείου. Είναι επίσης γνωστή ως καμπύλη Τακάγκι, από το όνομα του Τέιτζι Τακάγκι που την περιέγραψε το 1901, ή ως καμπύλη Τακάγκι-Λάντσμπεργκ, μια γενίκευση της καμπύλης που πήρε το όνομά της από τους Τακάγκι και Γκέοργκ Λάντσμπεργκ. Η ονομασία blancmange προέρχεται από την ομοιότητά της με την πουτίγκα Blancmange. Αποτελεί ειδική περίπτωση της γενικότερης καμπύλης Ντε Ραμ - βλέπε επίσης μορφοκλασματική καμπύλη.

Ορισμός

Η συνάρτηση blancmange ορίζεται στo μοναδιαίο διάστημα ως εξής

$\operatorname {blanc} (x)=\sum _{n=0}^{\infty }{s(2^{n}x) \over 2^{n}},$

όπου $s(x)$ είναι το τριγωνικό κύμα, που ορίζεται από τη σχέση $s(x)=\min _{n\in {\mathbf {Z} }}|x-n|$, δηλαδή, $s(x)$ είναι η απόσταση από το x μέχρι τον πλησιέστερο ακέραιο αριθμό.

Η καμπύλη Τακάγκι- Λάντσμπεργκ είναι μια μικρή γενίκευση, η οποία δίνεται από τη σχέση

$T_{w}(x)=\sum _{n=0}^{\infty }w^{n}s(2^{n}x)$

για μια παράμετρο $w$- έτσι η καμπύλη blancmange είναι η περίπτωση $w=1/2$. Η τιμή $H=-\log _{2}w$ είναι γνωστή ως Εκθέτης Χερστ.

Η συνάρτηση μπορεί να επεκταθεί σε όλη την πραγματική γραμμή: η εφαρμογή του ορισμού που δόθηκε παραπάνω δείχνει ότι η συνάρτηση επαναλαμβάνεται σε κάθε μοναδιαίο διάστημα.

Ορισμός λειτουργικής εξίσωσης

Η περιοδική εκδοχή της καμπύλης Τακάγκι μπορεί επίσης να οριστεί ως η μοναδική περιορισμένη λύση $T=T_{w}:\mathbb {R} \to \mathbb {R}$ στη λειτουργική εξίσωση

$T(x)=s(x)+wT(2x).$

Πράγματι, η συνάρτηση blancmange $T_{w}$ είναι ασφαλώς περιορισμένη και επιλύει τη συναρτησιακή εξίσωση, αφού

$T_{w}(x):=\sum _{n=0}^{\infty }w^{n}s(2^{n}x)=s(x)+\sum _{n=1}^{\infty }w^{n}s(2^{n}x)$$=s(x)+w\sum _{n=0}^{\infty }w^{n}s(2^{n+1}x)=s(x)+wT_{w}(2x).$

Αντιθέτως, αν $T:\mathbb {R} \to \mathbb {R}$ είναι μια περιορισμένη λύση της συναρτησιακής εξίσωσης, επαναλαμβάνοντας την ισότητα έχουμε για κάθε N

$T(x)=\sum _{n=0}^{N}w^{n}s(2^{n}x)+w^{N+1}T(2^{N+1}x)=\sum _{n=0}^{N}w^{n}s(2^{n}x)+o(1),{\text{ for }}N\to \infty ,$

οπότε $T=T_{w}$. Παρεμπιπτόντως, οι παραπάνω συναρτησιακές εξισώσεις διαθέτουν απείρως πολλές συνεχείς, μη περιορισμένες λύσεις, π.χ. $T_{w}(x)+c|x|^{-\log _{2}w}.$

Γραφική κατασκευή

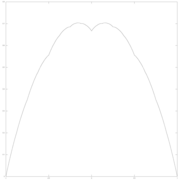
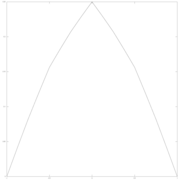
Η καμπύλη blancmange μπορεί να κατασκευαστεί οπτικά από τριγωνικές κυματοσυναρτήσεις, εάν το άπειρο άθροισμα προσεγγιστεί από πεπερασμένα αθροίσματα των πρώτων όρων. Στις παρακάτω εικόνες, προστίθενται στην καμπύλη σε κάθε στάδιο προοδευτικά λεπτότερες τριγωνικές συναρτήσεις (με κόκκινο χρώμα).

n = 0	n ≤ 1	n ≤ 2	n ≤ 3

Σχετικές δομές

Ως εναλλακτική λύση έχει προταθεί η καμπύλη Χίλμπερτ, καθώς έχει καλύτερη συμπεριφορά ως προς τη διατήρηση της τάξης και, μάλιστα, χρησιμοποιήθηκε σε ένα βελτιστοποιημένο δείκτη, τη S2-γεωμετρία.

Σύγκλιση και συνέχεια

Το άπειρο άθροισμα που ορίζει το $T_{w}(x)$ συγκλίνει απόλυτα για όλα τα $x$: αφού $0\leq s(x)\leq 1/2$ for all $x\in \mathbb {R}$, we have:

$\sum _{n=0}^{\infty }|w^{n}s(2^{n}x)|\leq {\frac {1}{2}}\sum _{n=0}^{\infty }|w|^{n}={\frac {1}{2}}\cdot {\frac {1}{1-|w|}}$ if $|w|<1.$

Επομένως, η καμπύλη Τακάγκι της παραμέτρου $w$ ορίζεται στο μοναδιαίο διάστημα (ή $\mathbb {R}$) αν $|w|<1$.

Η συνάρτηση Τακάγκι της παραμέτρου $w$ είναι συνεχής. Πράγματι, οι συναρτήσεις $T_{w,n}$ που ορίζονται από τα μερικά αθροίσματα $T_{w,n}(x)=\sum _{k=0}^{n}w^{k}s(2^{k}x)$ είναι συνεχείς και συγκλίνουν ομοιόμορφα προς την $T_{w}$, αφού:

$\left|T_{w}(x)-T_{w,n}(x)\right|=\left|\sum _{k=n+1}^{\infty }w^{k}s(2^{k}x)\right|=\left|w^{n+1}\sum _{k=0}^{\infty }w^{k}s(2^{k+n+1}x)\right|\leq {\frac {|w|^{n+1}}{2}}\cdot {\frac {1}{1-|w|}}$ για όλα x όταν $|w|<1.$

Αυτή η τιμή μπορεί να γίνει όσο μικρή θέλουμε επιλέγοντας μια αρκετά μεγάλη τιμή του n. Επομένως, σύμφωνα με το ομοιόμορφο οριακό θεώρημα, το $T_{w}$ είναι συνεχές αν |w| < 1.

• 
  parameter w = 2/3
• 
  parameter w = 1/2
• 
  parameter w = 1/3
• 
  parameter w = 1/4
• 
  parameter w = 1/8

Υποπροσθετικότητα

Αφού η απόλυτη τιμή είναι μια υποαδενική συνάρτηση, άρα είναι και η συνάρτηση $s(x)=\min _{n\in {\mathbf {Z} }}|x-n|$, και οι διαστολές της $s(2^{k}x)$- αφού οι θετικοί γραμμικοί συνδυασμοί και τα σημειακά όρια των υποαδενικών συναρτήσεων είναι υποαδενικά, η συνάρτηση Τακάγκι είναι υποαδενική για οποιαδήποτε τιμή της παραμέτρου $w$.

Η ειδική περίπτωση της παραβολής

Για $w=1/4$, προκύπτει η παραβολή: η κατασκευή της παραβολής με υποδιαίρεση του μέσου σημείου περιγράφηκε από τον Αρχιμήδη.

Διαφορετικότητα

Για τιμές της παραμέτρου $0<w<1/2$ η συνάρτηση Takagi $T_{w}$ είναι διαφορίσιμη με την κλασική έννοια σε κάθε $x\in \mathbb {R}$ που δεν είναι δυαδική λογική. Ακριβώς, με παραγώγιση υπό το πρόσημο της σειράς, για κάθε μη δυαδικό ορθολογικό $x\in \mathbb {R}$ βρίσκει κανείς

$T_{w}'(x)=\sum _{n=0}^{\infty }(2w)^{n}\,(-1)^{x_{-n-1}}$

όπου $(x_{n})_{n\in \mathbb {Z} }\in \{0,1\}^{\mathbb {Z} }$ είναι η ακολουθία δυαδικών ψηφίων στο ανάπτυγμα της βάσης 2 του $x$, δηλαδή $x=\sum _{n\in \mathbb {Z} }2^{n}x_{n}$. Επιπλέον, για αυτές τις τιμές του $w$ η συνάρτηση $T_{w}$ είναι Λιπσίτς με σταθερά $1 \over 1-2w$. Συγκεκριμένα για την ειδική τιμή $w=1/4$ βρίσκει κανείς, για κάθε μη δυαδικό ορθολογικό $x\in [0,1]$ $T_{1/4}'(x)=2-4x$, σύμφωνα με το αναφερθέν $T_{1/4}(x)=2x(1-x).$

Για $w=1/2$ η συνάρτηση blancmange $T_{w}$ είναι περιορισμένης μεταβολής σε κανένα μη κενό ανοικτό σύνολο- δεν είναι καν τοπικά Λιπσίτς, αλλά είναι οιονεί-Λιπσίτς, πράγματι, δέχεται τη συνάρτηση $\omega (t):=t(|\log _{2}t|+1/2)$ ως συντελεστή συνέχειας .

Αυτοομοιότητα

Ο αναδρομικός ορισμός επιτρέπει να δοθεί το μονοειδές των αυτοσυμμετριών της καμπύλης. Αυτό το μονοειδές δίνεται από δύο γεννήτριες, g και r, οι οποίες δρουν στην καμπύλη (περιορισμένη στο μοναδιαίο διάστημα) ως εξής

$[g\cdot T_{w}](x)=T_{w}\left({\frac {x}{2}}\right)={\frac {x}{2}}+wT_{w}(x)$

και

$[r\cdot T_{w}](x)=T_{w}(1-x)=T_{w}(x).$

Ένα γενικό στοιχείο του μονοειδούς έχει τότε τη μορφή $\gamma =g^{a_{1}}rg^{a_{2}}r\cdots rg^{a_{n}}$ για ορισμένους ακέραιους $a_{1},a_{2},\cdots ,a_{n}$ Αυτό δρα στην καμπύλη ως γραμμική συνάρτηση: $\gamma \cdot T_{w}=a+bx+cT_{w}$ για κάποιες σταθερές a, b και c. Επειδή η δράση είναι γραμμική, μπορεί να περιγραφεί με όρους ενός διανυσματικού χώρου, με βάση τον διανυσματικό χώρο:

$1\mapsto e_{1}={\begin{bmatrix}1\\0\\0\end{bmatrix}}$

$x\mapsto e_{2}={\begin{bmatrix}0\\1\\0\end{bmatrix}}$

$T_{w}\mapsto e_{3}={\begin{bmatrix}0\\0\\1\end{bmatrix}}$

Σε αυτή την αναπαράσταση, η δράση των g και r δίνεται από τις ακόλουθες σχέσεις

$g={\begin{bmatrix}1&0&0\\0&{\frac {1}{2}}&{\frac {1}{2}}\\0&0&w\end{bmatrix}}$

και

$r={\begin{bmatrix}1&1&0\\0&-1&0\\0&0&1\end{bmatrix}}$

Δηλαδή, η δράση ενός γενικού στοιχείου $\gamma$ απεικονίζει την καμπύλη blancmange στο μοναδιαίο διάστημα [0,1] σε ένα υποδιάστημα $[m/2^{p},n/2^{p}]$ για κάποιους ακέραιους m, n, p. Η απεικόνιση δίνεται ακριβώς από τη σχέση $[\gamma \cdot T_{w}](x)=a+bx+cT_{w}(x)$ όπου οι τιμές των a, b και c μπορούν να προκύψουν απευθείας από τον πολλαπλασιασμό των παραπάνω πινάκων. Αυτό σηµαίνει ότι:

$\gamma ={\begin{bmatrix}1&{\frac {m}{2^{p}}}&a\\0&{\frac {n-m}{2^{p}}}&b\\0&0&c\end{bmatrix}}$

Να σημειωθεί ότι $p=a_{1}+a_{2}+\cdots +a_{n}$ είναι άμεσο.

Το μονοειδές που παράγεται από τα g και r ονομάζεται μερικές φορές δυαδικό μονοειδές- είναι ένα υπομονοειδές της σπονδυλωτής ομάδας. Όταν συζητάμε τη σπονδυλωτή ομάδα, η πιο συνηθισμένη γραφή για τα g και r είναι T και S, αλλά αυτή η γραφή έρχεται σε σύγκρουση με τα σύμβολα που χρησιμοποιούνται εδώ.

Η παραπάνω τρισδιάστατη αναπαράσταση είναι μόνο μία από τις πολλές αναπαραστάσεις που μπορεί να έχει- δείχνει ότι η καμπύλη blancmange είναι μια πιθανή υλοποίηση της δράσης. Δηλαδή, υπάρχουν αναπαραστάσεις για οποιαδήποτε διάσταση, όχι μόνο για 3. Κάποιες από αυτές δίνουν τις καμπύλες Ντε Ραμ.

Ενσωμάτωση της καμπύλης Blancmange

Δεδομένου ότι το ολοκλήρωμα του $\operatorname {blanc} (x)$ από 0 έως 1 είναι 1/2, η ταυτότητα $\operatorname {blanc} (x)=\operatorname {blanc} (2x)/2+s(x)$ επιτρέπει τον υπολογισμό του ολοκληρώματος σε οποιοδήποτε διάστημα με την ακόλουθη σχέση. Ο υπολογισμός είναι αναδρομικός με χρόνο υπολογισμού της τάξης του λογαρίθμου της απαιτούμενης ακρίβειας. Ορισμός του

$I(x)=\int _{0}^{x}\operatorname {blanc} (y)\,dy$

ένα από αυτά έχει το εξής

$I(x)={\begin{cases}I(2x)/4+x^{2}/2&{\text{if }}0\leq x\leq 1/2\\1/2-I(1-x)&{\text{if }}1/2\leq x\leq 1\\n/2+I(x-n)&{\text{if }}n\leq x\leq (n+1)\\\end{cases}}$

Το οριστικό ολοκλήρωμα δίνεται από:

$\int _{a}^{b}\operatorname {blanc} (y)\,dy=I(b)-I(a).$

Μια πιο γενική έκφραση μπορεί να προκύψει με τον ορισμό

$S(x)=\int _{0}^{x}s(y)dy={\begin{cases}x^{2}/2,&0\leq x\leq {\frac {1}{2}}\\-x^{2}/2+x-1/4,&{\frac {1}{2}}\leq x\leq 1\\n/4+S(x-n),&(n\leq x\leq n+1)\end{cases}}$

το οποίο, σε συνδυασμό με την αναπαράσταση της σειράς, δίνει

$I_{w}(x)=\int _{0}^{x}T_{w}(y)dy=\sum _{n=0}^{\infty }(w/2)^{n}S(2^{n}x)$

Να σημειωθεί ότι

$I_{w}(1)={\frac {1}{4(1-w)}}$

Αυτό το ολοκλήρωμα είναι επίσης αυτο-ομοειδές στο μοναδιαίο διάστημα, κάτω από μια δράση του δυαδικού μονοειδούς που περιγράφεται στην ενότητα "Αυτοομοιότητα". Εδώ, η αναπαράσταση είναι 4-διάστατη, έχοντας τη βάση $\{1,x,x^{2},I(x)\}$. Αναδιατυπώνοντας τα παραπάνω για να γίνει πιο σαφής η δράση του g: στο μοναδιαίο διάστημα, έχουμε

$[g\cdot I_{w}](x)=I_{w}\left({\frac {x}{2}}\right)={\frac {x^{2}}{8}}+{\frac {w}{2}}I_{w}(x).$

Από αυτό μπορεί κανείς να διαβάσει άμεσα τις γεννήτριες της τετραδιάστατης αναπαράστασης:

$g={\begin{bmatrix}1&0&0&0\\0&{\frac {1}{2}}&0&0\\0&0&{\frac {1}{4}}&{\frac {1}{8}}\\0&0&0&{\frac {w}{2}}\end{bmatrix}}$

και

$r={\begin{bmatrix}1&1&1&{\frac {1}{4(1-w)}}\\0&-1&-2&0\\0&0&1&0\\0&0&0&-1\end{bmatrix}}$

Τα επαναλαμβανόμενα ολοκληρώματα μετασχηματίζονται σε αναπαράσταση 5,6,... διαστάσεων.

Σχέση με βασικό σχήμα

Έστω

$N={\binom {n_{t}}{t}}+{\binom {n_{t-1}}{t-1}}+\ldots +{\binom {n_{j}}{j}},\quad n_{t}>n_{t-1}>\ldots >n_{j}\geq j\geq 1.$

Ορισμός της συνάρτησης Κρούσκαλ-Κατόνα

$\kappa _{t}(N)={n_{t} \choose t+1}+{n_{t-1} \choose t}+\dots +{n_{j} \choose j+1}.$

Το θεώρημα Κρούσκαλ-Κατόνα δηλώνει ότι αυτός είναι ο ελάχιστος αριθμός (t − 1)-συμπλεγμάτων που είναι όψεις ενός συνόλου Ν t-συμπλεγμάτων.

Καθώς τα t και N πλησιάζουν στο άπειρο, $\kappa _{t}(N)-N$ (κατάλληλα κανονικοποιημένη) προσεγγίζει την καμπύλη blancmange.

Βιβλιογραφία

• Allaart, Pieter C.; Kawamura, Kiko (11 October 2011), The Takagi function: a survey 
• Lagarias, Jeffrey C. (17 December 2011), The Takagi Function and Its Properties 

Δημοσιεύσεις

• Weisstein, Eric W., "Blancmange Function" από το MathWorld.
• Takagi, Teiji (1901), «A Simple Example of the Continuous Function without Derivative», Proc. Phys.-Math. Soc. Jpn. 1: 176–177, doi:10.11429/subutsuhokoku1901.1.F176 
• Μπενουά Μάντελμπροτ, "Fractal Landscapes without creases and with rivers", appearing in The Science of Fractal Images, ed. Heinz-Otto Peitgen, Dietmar Saupe; Springer-Verlag (1988) pp 243–260.
• Linas Vepstas, Symmetries of Period-Doubling Maps, (2004)
• Donald Knuth, The Art of Computer Programming, volume 4a. Combinatorial algorithms, part 1. (ISBN 0-201-03804-8). See pages 372–375.

Δείτε επίσης

• Αλγόριθμος διαμαντιού τετραγώνου
• Καμπύλη που γεμίζει το χώρο
• Νιφάδα του Κοχ
• Καμπύλη Χίλμπερτ
• Καμπύλη του δράκου
• Σπόγγος του Μένγκερ

• Σύνολο Μάντελμπροτ
• Σύνολο Julia
• Σύνολο Κάντορ
• Οικοδομήσιμο Σύμπαν