Δέσμημα (γεωμετρία)

Ορισμένες γραμμές στο δέσμησμα μέσω του A

Στη γεωμετρία, το δέσμημα^[1] είναι μια οικογένεια γεωμετρικών αντικειμένων με μια κοινή ιδιότητα, όπως για παράδειγμα το σύνολο των ευθειών που διέρχονται από ένα δεδομένο σημείο σε ένα επίπεδο ή το σύνολο των κύκλων που διέρχονται από δύο δεδομένα σημεία σε ένα επίπεδο.

Αν και ο ορισμός του δεσμήματος είναι μάλλον ασαφής, το κοινό χαρακτηριστικό είναι ότι το δέσμημα καθορίζεται πλήρως από δύο οποιαδήποτε από τα μέλη της. Αντίστοιχα, ένα σύνολο γεωμετρικών αντικειμένων που προσδιορίζεται από τρία οποιαδήποτε μέλη του ονομάζεται δέσμη^[2]. Έτσι, το σύνολο όλων των ευθειών που διέρχονται από ένα σημείο στον τρισδιάστατο χώρο είναι δεσμήματα ευθειών, από τις οποίες δύο οποιεσδήποτε προσδιορίζουν ένα δεσμήμα ευθειών. Για να τονιστεί η δισδιάστατη φύση ενός τέτοιου δεσμήματος μερικές φορές αναφέρεται ως επίπεδο δέσμημα^[2].

Οποιοδήποτε γεωμετρικό αντικείμενο μπορεί να χρησιμοποιηθεί σε ένα δέσμημα. Τα συνηθισμένα είναι οι γραμμές, τα επίπεδα, οι κύκλοι, οι κωνικές, οι σφαίρες και οι γενικές καμπύλες. Ακόμη και σημεία μπορούν να χρησιμοποιηθούν. Ένα δέσμημα σημείων είναι το σύνολο όλων των σημείων σε μια δεδομένη γραμμή^[2] .

Δέσμημα γραμμών[Επεξεργασία | επεξεργασία κώδικα]

Σε ένα επίπεδο, έστω $u$ και $v$ δύο διαφορετικές γραμμές που τέμνονται. Για λόγους συγκεκριμενοποίησης, υποθέστε ότι η $u$ έχει την εξίσωση, $aX + bY + c = 0$ και $v$ την εξίσωση $a'X + b'Y + c' = 0$ . Τότε

λ u + μ v = 0

,

αντιπροσωπεύει, για κατάλληλα κλιμάκια $λ$ και $μ$ , κάθε ευθεία που διέρχεται από την τομή των $u$ = 0 και $v$ = 0. Αυτό το σύνολο των ευθειών που διέρχεται από ένα κοινό σημείο ονομάζεται δέσμημα ευθειών.^[3].

Σε ένα αφινικό επίπεδο με την αντανακλαστική παραλλαγή της παραλληλίας, ένα σύνολο παράλληλων ευθειών σχηματίζει μια κλάση ισοδυναμίας που ονομάζεται δέσμημα παράλληλων ευθειών.^[4] Αυτή η ορολογία είναι συνεπής με τον παραπάνω ορισμό, καθώς στη μοναδική προβολική επέκταση του αφινικού επιπέδου σε ένα προβολικό επίπεδο ένα μόνο σημείο (σημείο στο άπειρο) προστίθεται σε κάθε ευθεία στο δέσμημα παράλληλων ευθειών, καθιστώντας το έτσι ένα δέσμημα με την παραπάνω έννοια στο προβολικό επίπεδο.

Δέσμημα των επιπέδων[Επεξεργασία | επεξεργασία κώδικα]

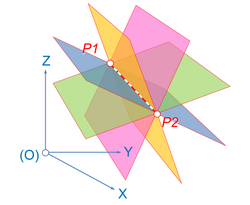
Το δέσμημα των επιπέδων, είναι το σύνολο των επιπέδων που διέρχονται από μια δεδομένη ευθεία γραμμή στον τρισδιάστατο χώρο, η οποία ονομάζεται άξονας του δεσμήματος. Το δέσμημα αναφέρεται μερικές φορές ως αξονική δέσμη^[5] ή βεντάλια επιπέδων ή δέσμη επιπέδων^[6]. Παραδείγματος χάριν, οι μεσημβρινοί του πλανήτη ορίζονται από τη δέσμη επιπέδων στον άξονα περιστροφής της Γης.

Δύο τέμνοντα επίπεδα συναντώνται σε μια ευθεία στον τρισδιάστατο χώρο, και έτσι, καθορίζουν τον άξονα και συνεπώς όλα τα επίπεδα του δεσμήματος.

Ο τετράχωρος χώρος των τετραδίων μπορεί να θεωρηθεί ως ένα αξονικό δέσμημα μιγαδικών επιπέδων που μοιράζονται όλα την ίδια πραγματική γραμμή. Στην πραγματικότητα, τα τετραδόνια (quaternions) περιέχουν μια σφαίρα φανταστικών μονάδων, και ένα ζεύγος αντιποδικών σημείων σε αυτή τη σφαίρα, μαζί με τον πραγματικό άξονα, δημιουργούν ένα μιγαδικό επίπεδο. Η ένωση όλων αυτών των μιγαδικών επιπέδων αποτελεί την 4-άλγεβρα των τετράδονιων.

Δέσμημα κύκλων[Επεξεργασία | επεξεργασία κώδικα]

Κάθε δύο κύκλοι στο επίπεδο έχουν έναν κοινό ριζικό άξονα, ο οποίος είναι η ευθεία που αποτελείται από όλα τα σημεία που έχουν την ίδια δύναμη ως προς τους δύο κύκλους. Ένα δέσμημα κύκλων (ή ομοαξονικό σύστημα) είναι το σύνολο όλων των κύκλων στο επίπεδο με τον ίδιο ριζικό άξονα^[7]. για να είναι περιεκτικό, οι ομόκεντροι κύκλοι λέγεται ότι έχουν ως ριζικό άξονα την ευθεία στο άπειρο.

Υπάρχουν πέντε τύποι δεσμημάτων κύκλων,^[8] οι δύο οικογένειες απολλώνιων κύκλων στην παραπάνω εικόνα αντιπροσωπεύουν δύο από αυτούς. Κάθε τύπος καθορίζεται από δύο κύκλους που ονομάζονται γεννήτριες του μολυβιού. Όταν περιγράφονται αλγεβρικά, είναι δυνατόν οι εξισώσεις να δέχονται φανταστικές λύσεις. Οι τύποι είναι οι εξής:

Ένα ελλειπτικό δέσμημα (κόκκινη οικογένεια κύκλων στο σχήμα) ορίζεται από δύο γεννήτορες που διέρχονται η μία από την άλλη σε ακριβώς δύο σημεία. Κάθε κύκλος ενός ελλειπτικού δεσμήματος διέρχεται από τα ίδια δύο σημεία. Ένα ελλειπτικό δέσμημα' δεν περιλαμβάνει φανταστικούς κύκλους.
Ένα υπερβολικό δέσμημα (μπλε οικογένεια κύκλων στο σχήμα) ορίζεται από δύο γεννήτορες που δεν τέμνουν ο ένας τον άλλον σε οποιοδήποτε σημείο. Περιλαμβάνει πραγματικούς κύκλους, φανταστικούς κύκλους και δύο εκφυλισμένους σημειακούς κύκλους που ονομάζονται σημεία Πονσελέ του δεσμήματος Κάθε σημείο στο επίπεδο ανήκει σε ακριβώς έναν κύκλο του δεσμήματος.
Ορίζεται ένα παραβολικό δέσμημα (ως οριακή περίπτωση) όπου δύο γεννήτορες κύκλοι εφάπτονται μεταξύ τους σε ένα μοναδικό σημείο. Αποτελείται από μια οικογένεια πραγματικών κύκλων, οι οποίοι εφάπτονται μεταξύ τους σε ένα μόνο κοινό σημείο. Ο εκφυλισμένος κύκλος με ακτίνα μηδέν στο σημείο αυτό ανήκει επίσης στο δέσμημα.
Μια οικογένεια ομόκεντρων κύκλων με κέντρο ένα κοινό κέντρο (μπορεί να θεωρηθεί ειδική περίπτωση υπερβολικού δεσμήματος όπου το άλλο σημείο είναι το σημείο στο άπειρο).
Η οικογένεια ευθειών που διέρχεται από ένα κοινό σημείο- αυτές θα πρέπει να ερμηνεύονται ως κύκλοι που όλοι διέρχονται από το σημείο στο άπειρο (μπορεί να θεωρηθεί ειδική περίπτωση ελλειπτικού δεσμήματος).^[9]^[10]

Ιδιότητες[Επεξεργασία | επεξεργασία κώδικα]

Ένας κύκλος που είναι ορθογώνιος προς δύο σταθερούς κύκλους είναι ορθογώνιος προς κάθε κύκλο στο δέσμημα που καθορίζουν.^[11]

Οι κύκλοι που είναι ορθογώνιοι προς δύο σταθερούς κύκλους σχηματίζουν ένα δέσμημα κύκλων.^[11]

Δύο κύκλοι προσδιορίζουν δύο δεσμήματα, το μοναδικό δέσμημα που τους περιέχει και το δέσμημα των κύκλων που είναι ορθογώνια προς αυτούς. Ο ριζικός άξονας του ενός δεσμήματος αποτελείται από τα κέντρα των κύκλων του άλλου δεσμήματος. Αν το ένα δέσμημα είναι ελλειπτικού τύπου, το άλλο είναι υπερβολικού τύπου και αντίστροφα.^[11]

Ο ριζικός άξονας οποιουδήποτε δεσμήματος κύκλων, που ερμηνεύεται ως κύκλος άπειρης ακτίνας, ανήκει στο δεσμήμα. Τρεις κύκλους ανήκουν σε ένα κοινό δέσμημα όταν και τα τρία ζεύγη έχουν τον ίδιο ριζικό άξονα και τα κέντρα τους είναι συγγραμμικά.

Προβολικός χώρος κύκλων[Επεξεργασία | επεξεργασία κώδικα]

Υπάρχει μια φυσική αντιστοιχία μεταξύ των κύκλων στο επίπεδο και των σημείων στον τρισδιάστατο προβολικό χώρο- μια γραμμή στον χώρο αυτό αντιστοιχεί σε μια μονοδιάστατη συνεχή οικογένεια κύκλων, επομένως ένα δέσμημα σημείων στον χώρο αυτό είναι ένα δέσμημα κύκλων στο επίπεδο.

Συγκεκριμένα, η εξίσωση ενός κύκλου ακτίνας $r$ με κέντρο ένα σημείο ( $p, q$ ),

(x-p)^{2}+(y-q)^{2}=r^{2},

μπορεί να αναδιατυπωθεί ως εξής

\alpha (x^{2}+y^{2})-2\beta x-2\gamma y+\delta =0,

όπου $α = 1, β = p, γ = q, και δ = p 2 + q 2 - r 2$ . Σε αυτή τη μορφή, ο πολλαπλασιασμός της τετραπλότητας ( $α,β,γ,δ$ ) με ένα βαθμωτό παράγει μια διαφορετική τετραπλότητα που αναπαριστά τον ίδιο κύκλο- έτσι, αυτές οι τετραπλότητες μπορούν να θεωρηθούν ως ομογενείς συντεταγμένες για το χώρο των κύκλων^[12]. Οι ευθείες μπορούν επίσης να αναπαρασταθούν με μια εξίσωση αυτού του τύπου στην οποία $α = 0$ και θα πρέπει να θεωρηθούν ως μια εκφυλισμένη μορφή κύκλου. Όταν $α \neq 0$ , μπορούμε να λύσουμε για $p = β/α, q = γ/α$ , και $r =\sqrt(p 2 + q 2 - δ/α)$ ; - ο τελευταίος τύπος μπορεί να δώσει $r = 0$ (οπότε ο κύκλος εκφυλίζεται σε σημείο) ή $r$ ίσο με φανταστικό αριθμό (οπότε το τετράγωνο ( $α,β,γ,δ$ ) λέγεται ότι αναπαριστά έναν φανταστικό κύκλο).

Το σύνολο των αφινικών συνδυασμών δύο κύκλων ( $α 1,β 1,γ 1,δ 1$ ), ( $α 2,β 2,γ 2,δ 2$ ), δηλαδή το σύνολο των κύκλων που αντιπροσωπεύονται από την τετράδα

z(\alpha _{1},\beta _{1},\gamma _{1},\delta _{1})+(1-z)(\alpha _{2},\beta _{2},\gamma _{2},\delta _{2})

για κάποια τιμή της παραμέτρου $z$ , σχηματίζει ένα δέσμημα - οι δύο κύκλοι είναι οι γεννήτριες του δεσμήματος.

Καρδιοειδές ως περίβλημα ενός δεσμήματος κύκλων[Επεξεργασία | επεξεργασία κώδικα]

Ένας άλλος τύπος δέσμημα κύκλων μπορεί να προκύψει ως εξής. Ας υποθέσουμε έναν δεδομένο κύκλο (που ονομάζεται κύκλος γεννήτριας) και ένα διακεκριμένο σημείο P στον κύκλο γεννήτριας. Το σύνολο όλων των κύκλων που διέρχονται από το P και έχουν το κέντρο τους στον κύκλο γεννήτριας σχηματίζουν ένα δέσμημα κύκλων. Το περίβλημα αυτού του δεσμήματος είναι καρδιοειδές.

Δέσμημα σφαιρών[Επεξεργασία | επεξεργασία κώδικα]

Μια σφαίρα προσδιορίζεται μοναδικά από τέσσερα σημεία που δεν είναι συνεπίπεδα. Γενικότερα, μια σφαίρα προσδιορίζεται μοναδικά από τέσσερις συνθήκες, όπως το να διέρχεται από ένα σημείο, να εφάπτεται σε ένα επίπεδο κ.λπ.^[13] Η ιδιότητα αυτή είναι ανάλογη με την ιδιότητα ότι τρία μη κολλητά σημεία προσδιορίζουν έναν μοναδικό κύκλο σε ένα επίπεδο.

Κατά συνέπεια, μια σφαίρα προσδιορίζεται μοναδικά από (δηλαδή περνάει από) έναν κύκλο και ένα σημείο που δεν βρίσκεται στο επίπεδο του κύκλου αυτού.

Εξετάζοντας τις κοινές λύσεις των εξισώσεων δύο σφαιρών, μπορεί να διαπιστωθεί ότι δύο σφαίρες τέμνονται σε έναν κύκλο και το επίπεδο που περιέχει αυτόν τον κύκλο ονομάζεται ριζικό επίπεδο των τεμνόμενων σφαιρών^[14] Αν και το ριζικό επίπεδο είναι πραγματικό επίπεδο, ο κύκλος μπορεί να είναι φανταστικός (οι σφαίρες δεν έχουν κανένα κοινό πραγματικό σημείο) ή να αποτελείται από ένα μόνο σημείο (οι σφαίρες εφάπτονται στο σημείο αυτό)^[15].

Αν $f (x, y, z) = 0$ and $g (x, y, z) = 0$ είναι οι εξισώσεις δύο διαφορετικών σφαιρών τότε

\lambda f(x,y,z)+\mu g(x,y,z)=0

είναι επίσης η εξίσωση μιας σφαίρας για αυθαίρετες τιμές των παραμέτρων $λ$ και $μ$ . Το σύνολο όλων των σφαιρών που ικανοποιούν αυτή την εξίσωση ονομάζεται δέσμημα σφαιρών που καθορίζεται από τις δύο αρχικές σφαίρες. Σε αυτόν τον ορισμό, μια σφαίρα μπορεί να είναι ένα επίπεδο (άπειρη ακτίνα, κέντρο στο άπειρο) και αν οι δύο αρχικές σφαίρες αποτελούν επίπεδα, τότε όλες οι σφαίρες στο δέσμημα αποτελούν επίπεδα, διαφορετικά υπάρχει μόνο ένα επίπεδο (το ριζικό επίπεδο) στο δέσμημα.^[16]

Αν το δέσμημα των σφαιρών δεν αποτελείται από όλα τα επίπεδα, τότε υπάρχουν τρεις τύποι δεσμημάτων:^[15]

Αν οι σφαίρες τέμνονται σε έναν πραγματικό κύκλο $C$ , τότε το δέσμημα αποτελείται από όλες τις σφαίρες που περιέχουν τον $C$ , συμπεριλαμβανομένου του ριζικού επιπέδου. Τα κέντρα όλων των συνηθισμένων σφαιρών του δεσμήματος βρίσκονται σε μια ευθεία που διέρχεται από το κέντρο του $C$ και είναι κάθετη στο ριζικό επίπεδο.
Αν οι σφαίρες τέμνονται σε έναν νοητό κύκλο, όλες οι σφαίρες του δεσμήματος διέρχονται επίσης από αυτόν τον νοητό κύκλο, αλλά ως συνηθισμένες σφαίρες είναι ασύνδετες (δεν έχουν κοινά πραγματικά σημεία). Η γραμμή των κέντρων είναι κάθετη στο ριζικό επίπεδο, το οποίο είναι ένα πραγματικό επίπεδο στο δέσμημα που περιέχει τον φανταστικό κύκλο.
Αν οι σφαίρες τέμνονται σε ένα σημείο $A$ , όλες οι σφαίρες στο μολύβι εφάπτονται στο $A$ και το ριζικό επίπεδο είναι το κοινό εφαπτόμενο επίπεδο όλων αυτών των σφαιρών. Η ευθεία των κέντρων είναι κάθετη στο ριζικό επίπεδο στο σημείο $A$ .

Όλες οι εφαπτόμενες γραμμές από ένα σταθερό σημείο του ριζικού επιπέδου στις σφαίρες ενός δεσμήματος έχουν το ίδιο μήκος.^[15]

Το ριζικό επίπεδο είναι ο τόπος των κέντρων όλων των σφαιρών που είναι ορθογώνια προς όλες τις σφαίρες ενός δεσμήματος. Επιπλέον, μια σφαίρα που είναι ορθογώνια σε δύο οποιεσδήποτε σφαίρες ενός δεσμήματος από σφαίρες είναι ορθογώνια σε όλες και το κέντρο της βρίσκεται στο ριζικό επίπεδο του δεσμήματος.^[15]

Δέσμημα των κωνικών[Επεξεργασία | επεξεργασία κώδικα]

Μια (μη εκφυλισμένη) κωνική προσδιορίζεται πλήρως από πέντε σημεία σε γενική θέση (όχι τρία συγγραμμικά) σε ένα επίπεδο και το σύστημα των κωνικών που περνούν από ένα σταθερό σύνολο τεσσάρων σημείων (πάλι σε επίπεδο και όχι τρία συγγραμμικά)) ονομάζεται δέσμημα κωνικών^[17]. Τα τέσσερα κοινά σημεία ονομάζονται σημεία βάσης του δεσμήματος. Από οποιοδήποτε σημείο εκτός από ένα σημείο βάσης, διέρχεται μία μόνο κωνική του δεσμήματος. Η έννοια αυτή γενικεύει το δέσμημα κύκλων.

Σε ένα προβολικό επίπεδο που ορίζεται πάνω σε ένα αλγεβρικά κλειστό πεδίο, οποιεσδήποτε δύο κωνικές συναντώνται σε τέσσερα σημεία (υπολογίζονται με πολλαπλότητα) και έτσι, προσδιορίζεται το δέσμημα των κωνικών με βάση αυτά τα τέσσερα σημεία. Επιπλέον, τα τέσσερα σημεία βάσης προσδιορίζουν τρία ζεύγη γραμμών (εκφυλισμένες κωνικές μέσω των σημείων βάσης, κάθε γραμμή του ζεύγους περιέχει ακριβώς δύο σημεία βάσης) και έτσι κάθε δέσμημα κωνικών θα περιέχει το πολύ τρεις εκφυλισμένες κωνικές^[18].

Ένα δέσμημα κωνικών μπορεί να αναπαρασταθεί αλγεβρικά με τον ακόλουθο τρόπο. Έστω $C 1$ και $C 2$ δύο διαφορετικές κωνικές σε ένα προβολικό επίπεδο που ορίζεται πάνω σε ένα αλγεβρικά κλειστό πεδίο $K$ . Για κάθε ζεύγος $λ, μ$ στοιχείων του $K$ , που δεν είναι και τα δύο μηδενικά, ισχύει η έκφραση:

\lambda C_{1}+\mu C_{2}

αντιπροσωπεύει μια κωνική στο δέσμημα που καθορίζεται από τα $C 1$ και $C 2$ . Αυτή η συμβολική αναπαράσταση μπορεί να υλοποιηθεί με μια μικρή κατάχρηση της σημειογραφίας (χρησιμοποιώντας την ίδια σημειογραφία για τον προσδιορισμό του αντικειμένου και της εξίσωσης που ορίζει το αντικείμενο). Αν θεωρήσουμε το $C 1$ , λόγου χάριν, ως μια τριμερή τετραγωνική μορφή, τότε το $C 1 = 0$ είναι η εξίσωση της "κωνικής $C 1$ ". Μια άλλη έμπρακτη υλοποίηση θα μπορούσε να προκύψει αν θεωρούσαμε το $C 1$ ως τον συμμετρικό πίνακα 3×3 που το αναπαριστά. Εάν οι $C 1$ και $C 2$ έχουν τέτοιες συγκεκριμένες υλοποιήσεις, τότε το ίδιο θα κάνει και κάθε μέλος του παραπάνω μολυβιού. Εφόσον το πλαίσιο χρησιμοποιεί ομογενείς συντεταγμένες σε προβολικό επίπεδο, δύο συγκεκριμένες αναπαραστάσεις (εξισώσεις ή πίνακες) δίνουν την ίδια κωνική αν διαφέρουν κατά μια μη μηδενική πολλαπλασιαστική σταθερά.

Δέσμημα επίπεδων καμπυλών[Επεξεργασία | επεξεργασία κώδικα]

Γενικότερα, ένα δέσμημα είναι η ειδική περίπτωση ενός γραμμικού συστήματος διαιρετών στο οποίο ο χώρος των παραμέτρων είναι μια προβολική γραμμή. Τυπικά δεσμήματα καμπυλών στο προβολικό επίπεδο, παραδείγματος χάριν, γράφονται ως εξής

\lambda C+\mu C'=0\,

όπου $C = 0$ , $C' = 0$ είναι επίπεδες καμπύλες.

Ιστορία[Επεξεργασία | επεξεργασία κώδικα]

Στον Ντεσαργκ αποδίδεται η επινόηση της έκφρασης "ordonnance de lignes" ^[19].

Ένας από τους πρώτους συγγραφείς της σύγχρονης προβολικής γεωμετρίας, ο G. B. Halsted (Χαλστεντ)^[20], εισήγαγε τους όρους "συνευθεία" και "επίπεδο δέσμημα" για να ορίσει τη γωνία: Οι ευθείες που διαθέτουν την ίδια διασταύρωση είναι συνευθεία. Το σύνολο όλων των συνεπίπεδων και συνεπίπεδων ευθειών ονομάζεται επίπεδο δέσμημα" και "Ένα κομμάτι του επίπεδου μολυβιού που οριοθετείται από δύο από τις ευθείες ως πλευρές ονομάζεται γωνία"^[21].

Δημοσιεύσεις[Επεξεργασία | επεξεργασία κώδικα]

Albert, Abraham Adrian (2016), Solid Analytic Geometry, Dover, ISBN 978-0-486-81026-3
Artin, E. (1957), Geometric Algebra, Interscience Publishers
Faulkner, T. E. (1952), Projective Geometry (2nd έκδοση), Edinburgh: Oliver and Boyd, ISBN 9780486154893, https://books.google.com/books?id=3TwCIg_O2yMC
Halsted, George Bruce (1906), Synthetic Projective Geometry, New York Wiley, https://archive.org/details/syntheticproject00halsuoft
Johnson, Roger A. (2007), Advanced Euclidean Geometry, Dover, ISBN 978-0-486-46237-0
Pedoe, Dan (1988), Geometry /A Comprehensive Course, Dover, ISBN 0-486-65812-0
Pfeifer, Richard E.; Van Hook, Cathleen (1993), «Circles, Vectors, and Linear Algebra», Mathematics Magazine 66 (2): 75–86, doi:10.2307/2691113
Samuel, Pierre (1988), Projective Geometry, Undergraduate Texts in Mathematic (Readings in Mathematics), New York: Springer-Verlag, ISBN 0-387-96752-4, https://archive.org/details/projectivegeomet0000samu
Schwerdtfeger, Hans (1979), Geometry of Complex Numbers: Circle Geometry, Moebius Transformation, Non-Euclidean Geometry, Dover, σελ. 8–10 .
Young, John Wesley (1971), Projective Geometry, Carus Monograph #4, Mathematical Association of America
Woods, Frederick S. (1961), Higher Geometry / An introduction to advanced methods in analytic geometry, Dover

Δείτε επίσης[Επεξεργασία | επεξεργασία κώδικα]

Regular ring (in commutative algebra)

Εξωτερικοί σύνδεσμοι[Επεξεργασία | επεξεργασία κώδικα]

English - Greek Dictionary of Pure and Applied Mathematics Εθνικό Μετσόβιο Πολυτεχνείο
Αγγλοελληνικό Λεξικό Μαθηματικής Ορολογίας - Πανεπιστήμιο Κύπρου
Commutative Ring Theory
Rings Close to Regular
Modules over Commutative Regular Rings

Παραπομπές[Επεξεργασία | επεξεργασία κώδικα]

↑ «English - Greek Dictionary of Pure and Applied Mathematics Εθνικό Μετσόβιο Πολυτεχνείο - Volume 2 - σελίδα 83» (PDF).
↑ ^2,0 ^2,1 ^2,2 Young 1971, p. 40
↑ Pedoe 1988, p. 106
↑ Artin 1957, p. 53
↑ Halsted 1906, σελ. 9
↑ Woods 1961, p. 12
↑ Johnson 2007, p. 34
↑ Some authors combine types and reduce the list to three. Schwerdtfeger (1979, pp. 8–10)
↑ Johnson 2007, p. 36
↑ Schwerdtfeger 1979, σελίδες 8–10
↑ ^11,0 ^11,1 ^11,2 Johnson 2007, p. 37
↑ Pfeifer & Van Hook 1993.
↑ Albert 2016, p. 55.
↑ Albert 2016, p. 57.
↑ ^15,0 ^15,1 ^15,2 ^15,3 Woods 1961, p. 267.
↑ Woods 1961, p. 266
↑ Faulkner 1952, pg. 64.
↑ Samuel 1988, pg. 50.
↑ Earliest Known Uses of Some Words of Mathematics, http://jeff560.tripod.com/p.html, ανακτήθηκε στις July 14, 2020
↑ «George Halsted - Biography». Maths History (στα Αγγλικά). Ανακτήθηκε στις 18 Μαΐου 2024.
↑ Halsted 1906, σελ. 9

Σημειώσεις[Επεξεργασία | επεξεργασία κώδικα]

H. Matsumura, Commutative algebra 1980 (ISBN 0-8053-7026-9).
Nagata, Masayoshi (1956), «On the chain problem of prime ideals», Nagoya Math. J. 10: 51–64, doi:10.1017/S0027763000000076, http://projecteuclid.org/euclid.nmj/1118799769
Nagata, Masayoshi (1962), Local rings, Interscience Tracts in Pure and Applied Mathematics, 13, New York-London: Interscience Publishers, a division of John Wiley & Sons ; reprinted by R. E. Krieger Pub. Co (1975) (ISBN 0-88275-228-6)

[1] «English - Greek Dictionary of Pure and Applied Mathematics Εθνικό Μετσόβιο Πολυτεχνείο - Volume 2 - σελίδα 83» (PDF).

[Young40-2] 2,0 ^2,1 ^2,2 Young 1971, p. 40

[3] Pedoe 1988, p. 106

[4] Artin 1957, p. 53

[5] Halsted 1906, σελ. 9

[6] Woods 1961, p. 12

[7] Johnson 2007, p. 34

[8] Some authors combine types and reduce the list to three. Schwerdtfeger (1979, pp. 8–10)

[9] Johnson 2007, p. 36

[10] Schwerdtfeger 1979, σελίδες 8–10

[Jo37-11] 11,0 ^11,1 ^11,2 Johnson 2007, p. 37

[12] Pfeifer & Van Hook 1993.

[13] Albert 2016, p. 55.

[14] Albert 2016, p. 57.

[Woods267-15] 15,0 ^15,1 ^15,2 ^15,3 Woods 1961, p. 267.

[Woods266-16] Woods 1961, p. 266

[17] Faulkner 1952, pg. 64.

[18] Samuel 1988, pg. 50.

[19] Earliest Known Uses of Some Words of Mathematics, http://jeff560.tripod.com/p.html, ανακτήθηκε στις July 14, 2020

[20] «George Halsted - Biography». Maths History (στα Αγγλικά). Ανακτήθηκε στις 18 Μαΐου 2024.

[21] Halsted 1906, σελ. 9

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]