Ισοσκελές τρίγωνο

Ισοσκελές τρίγωνο με

\mathrm {AB} =\mathrm {A\Gamma }

και

{\hat {\mathrm {B} }}={\hat {\mathrm {\Gamma } }}

.

Η διάμεσος, το ύψος και η διχοτόμος της

{\hat {\mathrm {A} }}

ταυτίζονται.

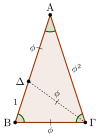
Στην γεωμετρία, ένα ισοσκελές τρίγωνο είναι ένα τρίγωνο του οποίου δύο πλευρές (και γωνίες) είναι ίσες μεταξύ τους. Για παράδειγμα, στο σχήμα το τρίγωνο $\mathrm {AB\Gamma }$ έχει $\mathrm {AB} =\mathrm {A\Gamma }$ και επομένως είναι ισοσκελές. Χαρακτηριστική ιδιότητα των ισοσκελών τριγώνων είναι ότι η διάμεσος, το ύψος και η διχοτόμος της κορυφής $\mathrm {A}$ ταυτίζονται.

Ειδική περίπτωση ισοσκελούς τριγώνου είναι το ισόπλευρο τρίγωνο που έχει όλες τις πλευρές (και γωνίες ίσες).

Ιδιότητες[Επεξεργασία | επεξεργασία κώδικα]

Στα ισοσκελή τρίγωνα ισχύουν οι παρακάτω ιδιότητες:^[1]^[2]^[3]^[4]

Ένα τρίγωνο είναι ισοσκελές ανν οι προσκείμενες στη βάση γωνίες του είναι ίσες.

Απόδειξη

( $\Rightarrow$ ) Θεωρούμε το ισοσκελές τρίγωνο $\mathrm {AB\Gamma }$ , όπου $\mathrm {AB} =\mathrm {A\Gamma }$ . Φέρνουμε τη διχοτόμο $\mathrm {A\Delta }$ . Τα τρίγωνα $\mathrm {AB\Delta }$ και $\mathrm {A\Gamma \Delta }$ είναι τότε ίσα σύμφωνα με το κριτήριο πλευράς-γωνίας-πλευράς, επομένως θα είναι ${\hat {\mathrm {B} }}={\hat {\mathrm {\Gamma } }}$ (ισότητα γωνιών).

( $\Leftarrow$ ): Θεωρούμε το τρίγωνο $\mathrm {AB\Gamma }$ με ${\hat {\mathrm {B} }}={\hat {\mathrm {\Gamma } }}$ . Φέρνουμε το ύψος $\mathrm {AH}$ του τριγώνου από την κορυφή $\mathrm {A}$ . Τα τρίγωνα $\mathrm {AHB}$ και $\mathrm {AH\Gamma }$ έχουν δύο γωνίες ίσες και μία αντίστοιχη πλευρά ίση. Επομένως, από το κριτήριο γωνίας-πλευράς-γωνίας έχουμε ότι τα τρίγωνα είναι ίσα. Συνεπώς, $\mathrm {AB} =\mathrm {A\Gamma }$ .

Σε ένα ισοσκελές τρίγωνο $\mathrm {AB\Gamma }$ με $\mathrm {AB} =\mathrm {A\Gamma }$ η διάμεσος $\mu _{\alpha }$ , η διχοτόμος $\delta _{\alpha }$ , το ύψος του $u_{\alpha }$ και η ευθεία του Όιλερ του τριγώνου ταυτίζονται.

Απόδειξη

Το ισοσκελές τρίγωνο έχει 2 πλευρές ίσες. Φέρνοντας τη διάμεσο του προς τη βάση του παρατηρούμε ότι δημιουργούνται 2 τρίγωνα που έχουν όλες τις πλευρές τους ίσες, επομένως και τα τρίγωνα είναι ίσα. Οι δύο γωνίες που δημιουργούνται από τη διάμεσο και τη βάση είναι ίσες και παραπληρωματικές, άρα είναι ορθές, δηλαδή η διάμεσος είναι και ύψος. Επίσης λόγω της ισότητας των τριγώνων οι δύο γωνίες που έχει σχηματίσει η διάμεσος στην κορυφή του τριγώνου είναι ίσες, άρα η διάμεσος είναι και διχοτόμος της γωνίας που βαίνει στη βάση. Επειδή τώρα σε μία πλευρά τριγώνου αντιστοιχεί μοναδική διάμεσος, μοναδικό ύψος και στη γωνία που βαίνει σε μια πλευρά τριγώνου αντιστοιχεί μοναδική διχοτόμος, η παραπάνω απόδειξη αρκεί για να πούμε ότι η διχοτόμος της γωνίας με κορυφή την κορυφή ισοσκελούς τριγώνου είναι και το ύψος και η διάμεσος προς τη βάση του καθώς και για το ότι το ύψος προς τη βάση ισοσκελούς τριγώνου διχοτομεί την γωνία της κορυφής και είναι διάμεσος προς τη βάση.

Σε ένα ισοσκελές τρίγωνο η ευθεία εκτός του περίκεντρου, ορθόκεντρου και βαρυκέντρου περιλαμβάνει και το έγκεντρο του τριγώνου.

Ένα τρίγωνο είναι ισοσκελές ανν η διχοτόμος της $\mathrm {A}$ είναι και ύψος.

Ένα τρίγωνο είναι ισοσκελές ανν η διχοτόμος της $\mathrm {A}$ είναι και διάμεσος.

Ένα τρίγωνο είναι ισοσκελές ανν η διάμεσος που αντιστοιχεί στην κορυφή $\mathrm {A}$ είναι και ύψος.

Ένα τρίγωνο είναι ισοσκελές ανν δύο ύψη είναι ίσα.

(Θεώρημα Steiner–Lehmus) Ένα τρίγωνο είναι ισοσκελές ανν δύο διχοτόμοι είναι ίσες.

Μετρικές σχέσεις[Επεξεργασία | επεξεργασία κώδικα]

Το ύψος που αντιστοιχεί στην κορυφή $\mathrm {A}$ δίνεται από

u_{\alpha }={\sqrt {\beta ^{2}-\left({\tfrac {\alpha }{2}}\right)^{2}}}

.

Απόδειξη

Έστω $\mathrm {AH}$ το ύψος που αντιστοιχεί στην $\mathrm {A}$ τότε από τις παραπάνω ιδιότητες είναι και διάμεσος, άρα $\mathrm {BH} =\mathrm {\Gamma H} ={\tfrac {\alpha }{2}}$ . Επομένως στο ορθογώνιο τρίγωνο $\mathrm {ABM}$ από το Πυθαγόρειο θεώρημα έχουμε ότι

u_{a}^{2}=\mathrm {AM} ^{2}+\mathrm {MB} ^{2}\Rightarrow u_{a}={\sqrt {\beta ^{2}+\left({\tfrac {\alpha }{2}}\right)^{2}}}

.

Το εμβαδόν του τριγώνου δίνεται από

\mathrm {E} ={\tfrac {\alpha }{2}}\cdot u_{\alpha }={\tfrac {\alpha }{2}}\cdot {\sqrt {\beta ^{2}-\left({\tfrac {\alpha }{2}}\right)^{2}}}

και

\mathrm {E} ={\tfrac {1}{2}}\cdot \alpha ^{2}\cdot \sin \phi

,

όπου

\phi

η γωνία προσκείμενη στη βάση

\alpha

.

Η ακτίνα του περιγεγραμμένου κύκλου δίνεται από

R={\frac {\beta ^{2}}{2{\sqrt {\beta ^{2}-\left({\tfrac {\alpha }{2}}\right)^{2}}}}}

.

Απόδειξη

Από τον νόμο των ημιτόνων έχουμε ότι

R={\frac {\beta }{2\sin {\hat {\mathrm {B} }}}}.

Από το ορθογώνιο τρίγωνο με το ύψος $\mathrm {AH}$ , έχουμε ότι

\sin {\hat {\mathrm {B} }}={\frac {\sqrt {\beta ^{2}-\left({\tfrac {\alpha }{2}}\right)^{2}}}{2\beta }}.

Συνδυάζοντας τις παραπάνω δύο σχέσεις λαμβάνουμε το ζητούμενο.

Η πλευρά του εγγεγραμμένου τετραγώνου με μία πλευρά πάνω στην βάση του τριγώνου είναι

S={\frac {\alpha \cdot u_{\alpha }}{\alpha +u_{\alpha }}}

.

Ειδικά ισοσκελή τρίγωνα[Επεξεργασία | επεξεργασία κώδικα]

Ορθογώνιο και ισοσκελές[Επεξεργασία | επεξεργασία κώδικα]

Το ισοσκελές ορθογώνιο τρίγωνο έχει τις εξής ιδιότητες:

Οι προσκείμενες γωνίες είναι 45°.
Η υποτείνουσα έχει μήκος $x{\sqrt {2}}$ αν $x$ το μήκος των δύο κάθετων πλευρών.
Το εμβαδόν του είναι ${\tfrac {1}{2}}x^{2}$ .
Προκύπτει ως το μισό ενός τετραγώνου (το $\mathrm {AB\Delta \Gamma }$ στο σχήμα).

Ισόπλευρο τρίγωνο[Επεξεργασία | επεξεργασία κώδικα]

Το ισόπλευρο τρίγωνο έχει τις εξής ιδιότητες:

Όλες οι πλευρές του είναι ίσες.
Όλες οι γωνίες είναι $60^{o}$ μοίρες.
Το εμβαδόν του τριγώνου είναι ${\tfrac {x{\sqrt {3}}}{4}}$ , όπου $x$ το μήκος των πλευρών.

Τρίγωνο με γωνίες 30-30-120[Επεξεργασία | επεξεργασία κώδικα]

To ισοσκελές τρίγωνο $\mathrm {AB\Gamma }$ με γωνίες ${\hat {\mathrm {A} }}=120^{o}$ και ${\hat {\mathrm {B} }}={\hat {\mathrm {\Gamma } }}=30^{o}$ έχει ενδιαφέρουσες ιδιότητες αρκετές από τις οποίες προκύπτουν από το γεγονός ότι μπορεί να χωριστεί σε τρία τρίγωνα εκ των οποίων το ένα είναι ισόπλευρο και τα άλλα δύο είναι ισοσκελή και όμοια με το αρχικό.

Ισοσκελές τρίγωνο με

{\hat {\mathrm {B} }}={\hat {\mathrm {\Gamma } }}=80^{o}

.

Η ιδιότητα του τριγώνου να υποδιαιρείται σε τέσσερα ισοσκελή τρίγωνα.

Τρίγωνο με γωνίες 80-80-20[Επεξεργασία | επεξεργασία κώδικα]

Το ισοσκελές τρίγωνο $\mathrm {AB\Gamma }$ με γωνίες ${\hat {\mathrm {A} }}=20^{o}$ και ${\hat {\mathrm {B} }}={\hat {\mathrm {\Gamma } }}=80^{o}$ έχει αρκετές ενδιαφέρουσες ιδιότητες.^[5]^[6]^[7] Μία από αυτές είναι η ιδιότητα ότι υποδιαιρείται σε τέσσερα ισοσκελή τρίγωνα με πλευρά ίση με την βάση του.^[8] H Roza Leiki ισοσκελή τρίγωνα στα οποία ισχύουν γενικεύσεις των ιδιοτήτων αυτών των τριγώνων.^[9]

Το χρυσό τρίγωνο με γωνίες

{\hat {\mathrm {A} }}=36^{o}

και

{\hat {\mathrm {B} }}={\hat {\mathrm {\Gamma } }}=72^{o}

.

Η ιδιότητα του τριγώνου να υποδιαιρείται σε δύο ισοσκελή τρίγωνα.

Χρυσό τρίγωνο[Επεξεργασία | επεξεργασία κώδικα]

Το χρυσό τρίγωνο είναι το ισοσκελές τρίγωνο με πλευρές $\phi ,\phi ^{2}$ και $\phi ^{2}$ , όπου $\phi$ η χρυσή τομή. Το τρίγωνο αυτό είναι το ένα δέκατο ενός δεκαγώνου. Έχει διάφορες ιδιότητες,^[10] όπως το ότι μπορεί να διαιρεθεί σε δύο ισοσκελή τρίγωνα όπως φαίνεται στο δεύτερο σχήμα.

Περαιτέρω θέματα[Επεξεργασία | επεξεργασία κώδικα]

Χορδή κύκλου[Επεξεργασία | επεξεργασία κώδικα]

Οι μετρικές σχέσεις μίας χορδής $\mathrm {AB}$ (για παράδειγμα η απόστασή της από το κέντρο του κύκλου) προκύπτουν θεωρώντας το ισοσκελές τρίγωνο $\mathrm {OAB}$ , όπου $\mathrm {OA} =\mathrm {OB}$ ως ακτίνες του κύκλου.

Διαίρεση τριγώνου σε ισοσκελή τρίγωνα[Επεξεργασία | επεξεργασία κώδικα]

Ένα οξυγώνιο τρίγωνο $\mathrm {AB\Gamma }$ μπορεί να χωριστεί σε τρία ισοσκελή τρίγωνα, χρησιμοποιώντας το κέντρο $\mathrm {O}$ του περιγεγραμμένου του κύκλου.^[11]

Οι διάγωνιοι ενός ορθογωνίου το χωρίζουν σε τέσσερα ισοσκελή τρίγωνα.

Κάθε μία από τις διαγώνιους ενός ρόμβου τον χωρίζει σε δύο ίσα τμήματα.

Ορθογώνιο παραλληλόγραμμο και Ρόμβος[Επεξεργασία | επεξεργασία κώδικα]

Οι διαγώνιοι ενός ορθογωνίου παραλληλογράμμου είναι ίσες και διχοτομούνται, επομένως δημιουργούν τέσσερα ισοσκελή τρίγωνα, τα $\mathrm {ABO} ,\mathrm {B\Gamma O} ,\mathrm {\Gamma \Delta O}$ και $\mathrm {\Delta AO}$ .

Αντίστοιχα, σε έναν ρόμβο κάθε μία από τις διαγώνιους του τον χωρίζουν σε δύο ισοσκελή τρίγωνα.

Πλακόστρωση tetrakis

Πλακόστρωση triakis

Πλακοστρώσεις[Επεξεργασία | επεξεργασία κώδικα]

Ορισμένα ισοσκελή τρίγωνα χρησιμοποιούνται για να πλακοστρώσουν το επίπεδο, όπως η πλακόστρωση tetrakis που χρησιμοποιεί ορθογώνια και ισοσκελή τρίγωνα ή η πλακόστρωση triakis που χρησιμοποιεί τα ισοσκελή τρίγωνα με γωνίες 30-30-120.

Εφαρμογές[Επεξεργασία | επεξεργασία κώδικα]

Σημαία της Γουιάνας

Σημαία της Αγίας Λουκίας

Γραφιστική[Επεξεργασία | επεξεργασία κώδικα]

Οι σημαίες κάποιων χωρών, καθώς και τα σήματα διαφόρων εταιρειών και οργανισμών έχουν ισοσκελή τρίγωνα για αισθητικούς λόγους.

Ισοσκελές τρίγωνο στην Παναγία των Παρισίων.

Οι γέφυρες ζευκτών τύπου Howe και Pratt.

Αρχιτεκτονική/Μηχανική[Επεξεργασία | επεξεργασία κώδικα]

Στην αρχιτεκτονική και την μηχανική το ισοσκελές τρίγωνο χρησιμοποιείται σε αρκετές κατασκευές. Για παράδειγμα, το σχήμα των στεγών, στις διατάξεις των δοκών στις γέφυρες και σε τμήματα εκκλησιών.

Δείτε επίσης[Επεξεργασία | επεξεργασία κώδικα]

Παραπομπές[Επεξεργασία | επεξεργασία κώδικα]

↑ Ταβναλης, Χ. Επίπεδος Γεωμετρία. Αθήνα: Ι. Χιωτελη.
↑ Νικολάου, Νικόλαος Δ. (1973). Θεωρητική Γεωμετρία. 1973: Οργανισμός εκδόσεως διδακτικών βιβλίων.
↑ Κανέλλος, Σπ. Γ. (1975). Ευκλείδειος Γεωμετρία. Αθήνα 1975: Οργανισμός Εκδόσεων Διδακτικών Βιβλίων.
↑ Τόγκας, Πέτρος Γ. (1957). Θεωρητική Γεωμετρία. Αθήνα: Πέτρου Γ. Τόγκα.
↑ Langley, Edward M. (Οκτωβρίου 1922). «643. [K 1 . 9. b.»]. The Mathematical Gazette 11 (160): 173–173. doi:doi.org/10.2307/3604746. https://archive.org/details/sim_mathematical-gazette_1922-10_11_160/page/173.
↑ Bogomolny, Alexander. «The 80-80-20 Triangle». Cut the Knot. Ανακτήθηκε στις 4 Αυγούστου 2023.
↑ Rike, Tom. «An Intriguing Geometry Problem». Berkeley Math Circle. Ανακτήθηκε στις 4 Αυγούστου 2023.
↑ Bogomolny, Alexander. «Consecutive Isosceles Decomposition». Cut the Knot. Ανακτήθηκε στις 4 Αυγούστου 2023.
↑ Leikin, Roza (1 Μαΐου 2001). «Dividable Triangles—What Are They?». The Mathematics Teacher 94 (5): 392–398. doi:https://doi.org/10.5951/mt.94.5.0392. https://archive.org/details/sim_mathematics-teacher_2001-05_94_5/page/392.
↑ Bogomolny, Alexander. «Golden Ratio in Geometry». Cut the Knot. Ανακτήθηκε στις 4 Αυγούστου 2023.
↑ Lord, N. J. (Ιουνίου 1982). «Isosceles subdivisions of triangles». The Mathematical Gazette 66 (436): 136–137. doi:https://doi.org/10.2307/3617750. https://archive.org/details/sim_mathematical-gazette_1982-06_66_436/page/136.

Commons logo

Τα Wikimedia Commons έχουν πολυμέσα σχετικά με το θέμα
Ισοσκελές τρίγωνο

[Tav-1] Ταβναλης, Χ. Επίπεδος Γεωμετρία. Αθήνα: Ι. Χιωτελη.

[N73-2] Νικολάου, Νικόλαος Δ. (1973). Θεωρητική Γεωμετρία. 1973: Οργανισμός εκδόσεως διδακτικών βιβλίων.

[K75-3] Κανέλλος, Σπ. Γ. (1975). Ευκλείδειος Γεωμετρία. Αθήνα 1975: Οργανισμός Εκδόσεων Διδακτικών Βιβλίων.

[T57-4] Τόγκας, Πέτρος Γ. (1957). Θεωρητική Γεωμετρία. Αθήνα: Πέτρου Γ. Τόγκα.

[5] Langley, Edward M. (Οκτωβρίου 1922). «643. [K 1 . 9. b.»]. The Mathematical Gazette 11 (160): 173–173. doi:doi.org/10.2307/3604746. https://archive.org/details/sim_mathematical-gazette_1922-10_11_160/page/173.

[6] Bogomolny, Alexander. «The 80-80-20 Triangle». Cut the Knot. Ανακτήθηκε στις 4 Αυγούστου 2023.

[7] Rike, Tom. «An Intriguing Geometry Problem». Berkeley Math Circle. Ανακτήθηκε στις 4 Αυγούστου 2023.

[8] Bogomolny, Alexander. «Consecutive Isosceles Decomposition». Cut the Knot. Ανακτήθηκε στις 4 Αυγούστου 2023.

[9] Leikin, Roza (1 Μαΐου 2001). «Dividable Triangles—What Are They?». The Mathematics Teacher 94 (5): 392–398. doi:https://doi.org/10.5951/mt.94.5.0392. https://archive.org/details/sim_mathematics-teacher_2001-05_94_5/page/392.

[10] Bogomolny, Alexander. «Golden Ratio in Geometry». Cut the Knot. Ανακτήθηκε στις 4 Αυγούστου 2023.

[11] Lord, N. J. (Ιουνίου 1982). «Isosceles subdivisions of triangles». The Mathematical Gazette 66 (436): 136–137. doi:https://doi.org/10.2307/3617750. https://archive.org/details/sim_mathematical-gazette_1982-06_66_436/page/136.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]